＝－2(|x|－)²+≤.

22．(14分)已知f(x)是二次函数，不等式f(x)<0的解集是(0,5)，且f(x)在区间[－1,4]上的最大值是12.

(1)求f(x)的解析式．

(2)是否存在自然数m，使得方程f(x)+＝0在区间

(m，m+1)内有且只有两个不等的实数根？若存在，求出所有m的值；若不存在，请说明理由．

解：(1)∵f(x)是二次函数，且f(x)<0的解集是(0,5)，∴可设f(x)＝ax(x－5)(a>0)．

∴f(x)在区间[－1,4]上的最大值是f(－1)＝6a.由已知，得6a＝12.∴a＝2.

∴f(x)＝2x(x－5)＝2x²－10x(x∈R)．

(2)方程f(x)+＝0等价于方程2x³－10x²+37＝0.

设h(x)＝2x³－10x²+37，

则h′(x)＝6x²－20x＝2x(3x－10)．

当x∈(0，)时，h′(x)<0，h(x)是减函数；

当x∈(，+∞)时，h′(x)>0，h(x)是增函数．

∵h(3)＝1>0，h()＝－<0，h(4)＝5>0，

∴方程h(x)＝0在区间(3，)，(，4)内分别有唯一实数根，

而在区间(0,3)，(4，+∞)内没有实数根．

∴存在唯一的自然数m＝3，使得方程f(x)+＝0在区间(m，m+1)内有且只有两个不同的实数根．

21．(12分)已知函数f(x)＝2x²+mx－1，集合A＝{x|

log₂(x+2)≥log₂(x²+x+1)}，B＝{x|32x²－1≤1}．

(1)设f(x)≤0的解集为C，若C⊆(A∪B)，求m的取值范围；

(2)当m∈A，x∈B时，求证：|f(x)|≤.

解：由题意A＝[－1,1]，B＝[－，]，

∴A∪B＝[－1,1]．

(1)∵C＝{x|2x²+mx－1≤0}且C⊆(A∪B)，

∴不等式2x²+mx－1≤0的解集是[－1,1]的子集．

∵Δ＝m²+8>0，

∴只要即可，解得－1≤m≤1.

∴m的取值范围为[－1,1]．

(2)∵m∈A，x∈B，∴|m|≤1，x²≤.

∴|f(x)|＝|2x²－1+mx|≤|2x²－1|+|mx|

20．(12分)某工厂拟建一座平面图为矩形，面积为200 m²，高度一定的三段污水处理池(如下图)．由于受地形限制，其长、宽都不能超过16 m，如果池的外壁的建造费单价为400元/m，池中两道隔墙的建造费单价为248元/m，池底的建造费单价为80元/m²，试设计水池的长x和宽y(x>y)，使总造价最低，并求出这个最低造价．

解：设污水池长为x m，则宽为 m，且0<x≤16,0<≤16，两道隔墙与宽边平行时，造价较省，设总价为Q(x)，则Q(x)＝400(2x+2×)+248×2×+80×200＝800(x+)+16000≥1600+16000＝44800.

当且仅当x＝(x>0)，即x＝18时取等号，∴44800不是最小值．

又∵0<x≤16,0<≤16,12.5≤x≤16，而Q(x)在[12.5,16]上单调递减，

∴Q(x)≥Q(16)＝800(16+)+16000＝45000(元)．

故水池长为16 m，宽为12.5 m时，其总造价最低，最低造价为45000元．

19．(12分)(2009·绵阳二诊)已知f(x)＝x³+mx²－x+2(m∈R)．

(1)如果函数f(x)的单调递减区间为(－，1)，求函数f(x)的解析式；

(2)(理)若f(x)的导函数为f′(x)，对任意的x∈(0，+∞)，不等式f′(x)≥2xlnx－1恒成立，求实数m的取值范围．

(文)若f(x)的导函数为f′(x)，对任意的x∈(0，+∞)，不等式f′(x)≥2(1－m)恒成立，求实数m的取值范围．

解：(1)f′(x)＝3x²+2mx－1.

由题意f′(x)＝3x²+2mx－1<0的解集是(－，1)，

即3x²+2mx－1＝0的两根分别是－，1.

将x＝1或x＝－代入方程3x²+2mx－1＝0得m＝－1.

∴f(x)＝x³－x²－x+2.

(2)(理)由题意知3x²+2mx－1≥2xlnx－1在x∈

(0，+∞)时恒成立，即m≥lnx－x在x∈(0，+∞)时恒成立．

设h(x)＝lnx－，则h′(x)＝－.令h′(x)＝0，得x＝.

当0<x<时，h′(x)>0；当x>时，h′(x)<0，

∴当x＝时，h(x)取得最大值，h(x)_max＝ln－1＝ln2－ln3e，所以m≥ln2－ln3e.

因此m的取值范围是[ln2－ln3e，+∞)．

(文)由题意知3x²+2mx－1≥2(1－m)在x∈(0，+∞)时恒成立，即2mx+2m≥3－3x²，所以2m(x+1)≥3(1－x²)．

由于x∈(0，+∞)，于是2m≥3(1－x)，得m≥(1－x)．

而(1－x)<，所以m的取值范围为[，+∞)．

18．(12分)已知不等式log₂(ax²－3x+6)>2的解集是{x|x<1或x>b}．

(1)求a，b的值；

(2)解不等式>0(c为常数)．

解：(1)不等式log₂(ax²－3x+6)>2⇔ax²－3x+2>0，

由已知，该不等式的解集是{x|x<1或x>b}．

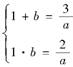∴，解得.

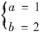(2)当a＝1，b＝2时，不等式>0变为>0.

∴<0，即(x－c)(x+2)<0.

∴当c<－2时，解集为(c，－2)；当c＝－2时，解集为空集；当c>－2时，解集为(－2，c)．

17．(12分)已知a，b，c为互不相等的正数，且abc＝1，

求证：++<++.

证明：证法1：∵a，b，c是不等正数，且abc＝1，

∴++＝++

<++＝++.

证法2：∵a，b，c是不等正数，且abc＝1，

∴++＝bc+ca+ab

＝++

>++

＝++.

16．(2009·江西高考)若不等式≤k(x+2)－的解集为区间[a，b]，且b－a＝2，则k＝________.

解析：在坐标系下画出函数y＝与y＝k(x+2)－的图象，结合图象，通过观察与分析可知，a＝1，b＝3，由此可知点(1,2)是函数y＝与y＝k(x+2)－的图象的交点，因此有2＝k(1+2)－，k＝.

答案：

15．若f(x)是R上的减函数，且f(x)的图象经过点A(0,3)和B(3，－1)，则不等式|f(x+1)－1|<2的解集是______．

解析：－1<f(x+1)<3，又f(0)＝3，f(3)＝－1，

所以f(3)<f(x+1)<f(0)，

又f(x)是减函数，所以0<x+1<3，－1<x<2.

答案：{x|－1<x<2}

14．已知函数f(x)＝sinx+5x，x∈(－1,1)若f(1－a)+

f(1－a²)<0，则a的取值范围是__________．

解析：由f(x)在(－1,1)上是单调递增的奇函数，由f(1－a)+f(1－a²)<0成立，转化为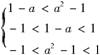⇒1<a<.

答案：(1，)

13．不等式2x－+1≤的解集为__________．

解析：依题意得，2x－+1≤2^－1，x－+1≤－1，即≤0，解得不等式的解集为{x|x≤－3或0<x≤1}．

答案：{x|x≤－3或0<x≤1}