10．(2009·福建质检)函数y＝的图象大致是　　　　　　　　　　　　　　　　　　　　　　　 (　)

解析：令x＝0，得y＝；令x＝1，得y＝1，

∴图象过(0，)，(1,1)两点，故选C.

答案：C

9．(2010·河南重点中学联考)已知函数f(x)是定义在(－2,2)上的奇函数，当x∈(0,2)时，f(x)＝2^x－1，则f(log₂)的值为　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．－2　 　　　　　　　　　　　　　　　　　　　　　　　　 B．－

C．2　 　　　　　　　　　　　　　　　　　　　　　　　　　　 D.－1

解析：当x∈(－2,0)时，－x∈(0,2)，又∵当x∈(0,2)时，f(x)＝2^x－1，∴f(－x)＝2^－x－1，又因函数f(x)是定义在(－2,2)上的奇函数，∴f(－x)＝－f(x)＝2^－x－1，

∴x∈(－2,0)时，f(x)＝1－.∵－2<log₂<0，

∴f(log₂)＝1－＝－2.故选A.

答案：A

8．定义在R上的偶函数f(x)＝f(x+2)，当x∈[3,4]时，f(x)＝x－2，则有　　　　　 (　)

A．f<f　 　　　　　　　　　　　　　　　　 B．f>f

C．f(sin1)<f(cos1)　 　　　　　　　　　　　　　　　　 D．f>f

解析：由f(x)＝f(x+2)知f(x)是周期为2的周期函数，又f(x)为偶函数，则f(x)在[0,1]上为减函数．因为0<sin<cos<1,0<cos<sin<1,0<cos1<sin1<1,0<cos<sin<1，所以只有f(sin1)<f(cos1)成立，故选C.

答案：C

7．若a＝2^0.6，b＝log_π3，c＝log₂sin，则　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．a>b>c　 　　　　　　　　　　　　　　　　　　　　　　 B．b>a>c

C．c>a>b　 　　　　　　　　　　　　　　　　　　　　　　 D．b>c>a

解析：∵a＝2^0.6>2⁰＝1；log_π1<log_π3<log_ππ，0<b<1；c＝log₂sinπ<log₂1＝0，∴a>b>c，选A.

答案：A

6．已知函数f(x)＝x³+m·2^x+n是奇函数，则　　　　　　　　　　　　　　　　　　　　　　 (　)

A．m＝0　 　　　　　　　　　　　　　　　　　　　　　　　　　　 B．m＝0且n＝0

C．n＝0　 　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．m＝0或n＝0

解析：根据f(0)＝0且f(－1)＝－f(1)求解．

答案：B

5．函数f(x)＝1+log₂x与g(x)＝2^－x+1在同一直角坐标系下的图象大致是(　)

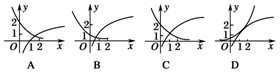
解析：f(x)＝1+log₂x的图象是由y＝log₂x的图象向上平移一个单位得到，g(x)＝2^－x+1当x＝0时，g(x)＝2.故选C.

答案：C

4．为了得到函数y＝2^x－3－1的图象，只需把函数y＝2^x的图象上所有的点(　)

A．向右平移3个单位长度，再向下平移1个单位长度

B．向左平移3个单位长度，再向下平移1个单位长度

C．向右平移3个单位长度，再向上平移1个单位长度

D．向左平移3个单位长度，再向上平移1个单位长度

答案：A

3．函数y＝log_a(3x－2)(a>0，a≠1)的图象过定点(　)

A.　 B．(1,0)

C．(0,1)　 D.

解析：令3x－2＝1可解得x＝1，即得函数y＝log_a(3x－2)

(a>0且a≠1)的图象过定点(1,0)，故选B.

答案：B

2．函数f(x)＝(x>1)的反函数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．y＝，x∈(0，+∞)　 　　　　　　　　　　　　　 B．y＝，x∈(1，+∞)

C．y＝，x∈(0,1)　 　　　　　　　　　　　　　　　　　 D．y＝，x∈(0,1)

解析：因为f(x)＝＝1－，x>1，所以f(x)∈(0,1)．由y＝得x＝，则f(x)＝(x>1)的反函数为f^－1(x)＝(0<x<1)，故选C.

答案：C

1．函数f(x)＝lg的定义域为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．{x|－2<x<1}　　　　　　　　　　　　　　　　　　　　　　 B．{x|x<－2或x>1}

C．{x|x>2} 　 　　　　　　　　　　　　　　　　　　　　　　　　 D．{x|－2<x<1或x>2}

解析：由>0⇒(x－1)(x－2)(x+2)>0，解得：x>2或－2<x<1，故选D.

答案：D