16．(2010·东北三校二模)已知直线ax+by+c＝0被曲线M：所截得的弦AB的长为2，O为原点，那么·的值等于__________．

解析：依题意，知曲线M是以原点为圆心，2为半径的圆，因为直线被圆截得的弦长为2，所以∠AOB＝60°，所以·＝||||cos60°＝2×2×＝2.

答案：2

15．(2009·石家庄二检)已知A、B是直线l同侧的两个定点，且到l的距离分别为a、b，点P是直线l上的一个动点，则|+3|的最小值是__________．

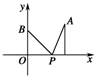
图4

解析：以直线l为x轴，点B在l上的射影O为坐标原点，建立如图4所示的直角坐标系，则B(0，b)，A(n，a)(n>0)，设P(x,0)，则+3＝(n－x，a)+3(－x，b)＝

(n－4x，a+3b)，|+3|²＝(n－4x)²+(a+3b)²，当n－4x＝0时，|+3|_min＝a+3b.

答案：a+3b

14．已知三个向量＝(k,12)，＝(4,5)，＝(10，k)，且A、B、C三点共线，则k＝__________.

解析：由A、B、C三点共线，可得＝λ，即(4－k，－7)＝λ(6，k－5)，于是得方程组

利用代入法解得或

答案：－2或11

13．如图3，已知＝3e₁，＝3e₂，C、D是AB的三等分点，则＝__________，＝__________.

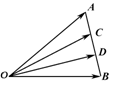
图3

解析：＝+＝+＝+(－)＝＝＝2e₁+e₂，

＝+＝+＝+(－)

＝＝

＝＝e₁+2e₂.

答案：2e₁+e₂　e₁+2e₂

12．(2010·东北三校一模)设a＝(a₁，a₂)，b＝(b₁，b₂)．定义一种向量积：a⊗b＝(a₁，a₂)⊗(b₁，b₂)＝(a₁b₁，a₂b₂)．已知m＝(2，)，n＝(，0)，点P(x，y)在y＝sinx的图象上运动，点Q在y＝f(x)的图象上运动，满足＝m⊗+n(其中O为坐标原点)，则y＝f(x)的最大值A及最小正周期T分别为

(　)

A．2，π 　　　　　　　　　　　　　 B．2,4π

C.，4π　 　　　　　　　　　　　　　 D.，π

解析：设Q(x₀，y₀)，＝(x₀，y₀)，＝(x，y)，∵＝m⊗+n，∴(x₀，y₀)＝(2，)⊗(x，y)+(，0)＝(2x，y)+(，0)＝(2x+，y)，∴

⇒代入y＝sinx中得，2y₀＝sin(x₀－)，所以y＝f(x)的表达式为y＝sin(x－)，所以最大值为，周期为4π，选C.

答案：C

11．(2010·湖北八校联考)在O点测量到远处有一物体在做匀速直线运动，开始时该物体位于P点，一分钟后，其位置在Q点，且∠POQ＝90°，再过二分钟后，该物体位于R点，且∠QOR＝60°，则tan²∠OPQ的值等于

(　)

A.　 　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　 D．以上均不正确

解析：以O为原点，OP为x轴，OQ为y轴建立直角坐标系，设P(m,0)，Q(0，n)，则有＝2，得R(－2m,3n)，由∠QOR＝60°，得

cos∠QOR＝＝OQ,\s\up6(→OR,\s\up6(→＝，

得27n²＝4m²，即tan²∠OPQ＝＝.故选C.

答案：C

10．(2009·合肥质检二)已知平面上不共线的四点O，A，B，C.若－3+2＝0，则AB,\s\up6(→\s\up7(　等于

(　)

A.　 　　　　　　　　　　　　　　　　 B.

C．1　 　　　　　　　　　　　　　　　 D．2

解析：+2＝0，∴＝2.

答案：D

9．(2009·福州质检)已知非零向量a、b，若a·b＝0，则＝

(　)

A.　 　　　　　　　　　　　　　　　　 B．2

C.　 　　　　　　　　　　　　　　　　　 D．1

解析：∵|a－2b|＝，|a+2b|＝，

∴＝1.

答案：D

8．(2009·郑州二检)已知A，B，C是平面上不共线的三点，O为平面ABC内任一点，动点P满足等式＝[(1－λ)+(1－λ)+(1+2λ)](λ∈R且λ≠0)，则点P的轨迹一定通过△ABC的

(　)

A．内心　 　　　　　　　　　　　　　 B．垂心

C．外心　 　　　　　　　　　　　　　 D．重心

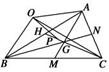
图2

解析：依题意，设△ABC的三边AB、BC、CA的中点分别为H、M、N，AM、CH、BN的交点为G.＝[(1－λ)+(1－λ)+(1+2λ)]＝[(1－λ)(+)+(1－λ)+(1+2λ)]＝[2(1－λ)(+)+(1－λ)+(1+2λ)]＝[3+2(1－λ)+(1－λ)]，所以－＝(2++)＝(+)＝，即＝，所以点P的轨迹一定通过△ABC的重心，选择D.

答案：D

7．若点P分有向线段所成的比为－，则点B分有向线段所成的比是

(　)

A．－　 　　　　　　　　　　　　　 B．－

C.　 　　　　　　　　　　　　　　　　　 D．3

解析：由已知条件可得点P在线段AB的反向延长线上，且AP,\s\up6(→\s\up7(　＝，因此向量与方向相反且PB,\s\up6(→\s\up7(　＝，故点B分有向线段所成的比是－，故选A.

答案：A