4．某小组共有8名同学，其中男生6人，女生2人，现从中按性别分层随机抽取4人参加一项公益活动，则不同的抽取方法有

(　)

A．40种　 　　　　　　　　　　　　　　　　　　　　　　　　　　 B．70种

C．80种　 　　　　　　　　　　　　　　　　　　　　　　　　　　 D．240种

解析：依题意得，所选出的4人必是3名男生、1名女生，因此满足题意的抽取方法共有CC＝40种，选A.

答案：A

3．五个人排成一排，甲、乙不相邻，且甲、丙也不相邻的不同排法的种数为

(　)

A．60　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．48

C．36　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．24

解析：五个人排成一排，其中甲、乙不相邻且甲、丙也不相邻的排法可分为两类：一类是甲、乙、丙互不相邻，此类方法有A·A＝12种(先把除甲、乙、丙外的两个人排好，有A种方法，再把甲、乙、丙插入其中，有A种方法，因此此类方法有A·A＝12种)；另一类是乙、丙相邻但不与甲相邻，此类方法有A·A·A＝24种方法(先把除甲、乙、丙外的两人排好，有A种方法，再从这两人所形成的三个空位中任选2个，作为甲和乙、丙的位置，此类方法有A·A·A＝24种)．综上所述，满足题意的方法种数共有12+24＝36，选C.

答案：C

2．(x+2)⁶的展开式中x³的系数为

(　)

A．20　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．40

C．80　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．160

解析：注意到(x+2)⁶的展开式的通项是T_r+1＝C·x^6－r·2^r＝C·2^r·x^6－r，令6－r＝3得r＝3.因此(x+2)⁶的展开式中x³的系数是C·2³＝160，选D.

答案：D

1．(2010·海淀期末)5个人分4张同样的足球票，每人至多分1张，而且票必须分完，那么不同的分法种数是

(　)

A．5⁴　　　　　　　　　　　　　　　　　　　 B．4⁵

C．5×4×3×2　 　　　　　　　　　　　　　　　　　　　　　 D.

解析：依题意得，不同的分法即是从5个人中选出4人来分，因此相应的方法数为C＝，选D.

答案：D

22．(14分)已知向量a＝(x,1)，b＝(1，－sinx)，函数f(x)＝a·b.

(1)若x∈[0，π]，试求函数f(x)的值域；

(2)(理)若θ为常数，且θ∈(0，π)，设g(x)＝－f()，x∈[0，π]，请讨论g(x)的单调性，并判断g(x)的符号．

解：(1)f(x)＝a·b＝x－sinx，

∴f′(x)＝1－cosx，x∈[0，π]．

∴f′(x)≥0.

∴f(x)在[0，π]上单调递增．

于是f(0)≤f(x)≤f(π)，即0≤f(x)≤π，

∴f(x)的值域为[0，π]．

(2)g(x)＝－+sin

＝－sinθ－sinx+sin，

∴g′(x)＝－cosx+cos.

∵x∈[0，π]，θ∈(0，π)，

∴∈(0，π)．而y＝cosx在[0，π]内单调递减，

∴由g′(x)＝0，得x＝，即x＝θ.

因此，当0≤x<θ时，g′(x)<0，g(x)单调递减；

当θ<x≤π时，g′(x)>0，g(x)单调递增．

由g(x)的单调性，知g(θ)是g(x)在[0，π]上的最小值，

∴当x＝θ时，g(x)＝g(θ)＝0；当x≠θ时，g(x)>g(θ)＝0.

综上知，当x∈[0，θ)时，g(x)单调递减；

当x∈(θ，π]时，g(x)单调递增；

当x＝θ时，g(x)＝0；

当x≠θ时，g(x)>0.

21．(12分)(2009·杭州质检)点O是梯形ABCD对角线的交点，|AD|＝4，|BC|＝6，|AB|＝2.设与同向的单位向量为a₀，与同向的单位向量为b₀.

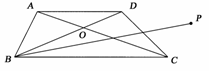
图5

(1)用a₀和b₀表示，和；

(2)若点P在梯形ABCD所在的平面上运动，且||＝2，求||的最大值和最小值．

解：(1)由题意知＝6a₀，＝2b₀，∴＝－＝6a₀－2b₀；

∵∥，∴＝4a₀，则＝+＝2b₀－6a₀+4a₀＝2b₀－2a₀；

∵AD∥BC，∴|OA|∶|OC|＝|AD|∶|BC|＝2∶3，

则＝－＝－(6a₀－2b₀)＝－a₀+b₀.

(2)由题意知点P是在以点C为圆心，2为半径的圆周上运动，所以由几何意义即得||的最大值和最小值分别应该为8和4.

20．(12分)(2009·重庆二次调研)有一道解三角形的题目，因纸张破损致使有一个条件不清，具体如下：

在△ABC中，已知a＝，B＝45°，________，求角A.

经推断，破损处的条件为三角形一边的长度，且答案提示角A＝60°，试将条件补充完整，并说明理由．

解：将角A＝60°看作已知条件，

由＝得b＝；由＝得c＝.

若已知条件为b＝，则由＝得sinA＝，

∴角A＝60°或120°，不合题意，舍去．

若已知条件为c＝，则由b²＝a²+c²－2accosB＝2得b＝，

∴cosA＝＝，∴角A＝60°，符合题意．

综上所述，破损处的已知条件应为c＝.

19．(12分)在△ABC中，已知内角A＝，边BC＝2.设内角B＝x，周长为y.

(1)求函数y＝f(x)的解析式和定义域；

(2)求y的最大值．

解：(1)△ABC的内角和A+B+C＝π，由A＝，B>0，C>0得0<B<.

应用正弦定理，知AC＝sinB＝sinx＝4sinx，

AB＝sinC＝4sin(－x)．

因为y＝AB+BC+AC，

所以y＝4sinx+4sin(－x)+2(0<x<)．

(2)因为y＝4(sinx+cosx+sinx)+2

＝4sin(x+)+2(<x+<)，

所以当x+＝，即x＝时，y取得最大值6.

18．(12分)已知向量a＝(3，－4)，求：

(1)与a平行的单位向量b；

(2)与a垂直的单位向量c；

(3)将a绕原点逆时针方向旋转45°得到的向量e的坐标．

解：(1)设b＝λa，则|b|＝1，

b＝(，－)或b＝(－，)．

(2)由a⊥c，a＝(3，－4)，可设c＝λ(4,3)，求得c＝(，)或c＝(－，－)．

(3)设e＝(x，y)，则x²+y²＝25.

又a·e＝3x－4y＝|a|·|e|cos45°，即3x－4y＝，由上面关系求得e＝(，－)或e＝(－，－)．

而向量e由a绕原点逆时针方向旋转45°得到，故e＝(，－)．

17．(12分)(2009·江西高考)在△ABC中，A，B，C所对的边分别为a，b，c，A＝，(1+)c＝2b.

(1)求C；

(2)若·＝1+，求a，b，c.

解：(1)由(1+)c＝2b，得＝+＝，

则有＝＝cotC+＝+，得cotC＝1，即C＝.

(2)由·＝1+，得abcosC＝1+；而C＝，即得ab＝1+，则有解得