8．将正方形ABCD沿对角线BD折成一个120°的二面角，点C到达点C₁，这时异面直线AD与BC₁所成的角的余弦值是

(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C. 　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　 D.

解析：由题意易知∠ABC₁即为AD与BC₁所成的角，解△ABC₁，得余弦为.

答案：D

7．已知球O的半径为1，A、B、C三点都在球面上，且每两点间的球面距离均为，则球心O到平面ABC的距离为

(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C. 　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析：设球心O到平面ABC的距离为h，由等体积法可知，V_O－ABC＝V_C－AOB，即h·S_△ABC＝OC·S_△AOB，即h＝＝＝.

答案：B

6．设M是正四面体ABCD的高线AH上一点，连结MB、MC，若∠BMC＝90°，则的值为

(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．1

解析：设正四面体的棱长为a，MH＝x，则MC²＝MB²＝MH²+BH²＝x²+a²，在Rt△BMC中，由MB²+MC²＝BC²，得2(x²+a²)＝a²，解得x＝a，∴AM＝MH＝AH，即＝1.

答案：D

5．正方体A′B′C′D′－ABCD的棱长为a，EF在AB上滑动，且|EF|＝b(b<a)，Q点在D′C′上滑动，则四面体A′－EFQ的体积为

(　)

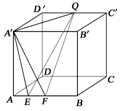
图1

A．与E、F位置有关

B．与Q位置有关

C．与E、F、Q位置都有关

D．与E、F、Q位置均无关，是定值

解析：V_A′－EFQ＝V_Q－A′EF.

答案：D

4．(2010·浙江温州八校联考)已知直线a，如果直线b同时满足条件①a与b异面；②a与b成定角；③a与b的距离为定值，则这样的直线b

(　)

A．唯一确定　 　　　　　　　　　　　　　　　　　　　　　　　 B．有2条

C．有4条　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．有无数条

解析：找出模型，如墙角处考虑D正确．

答案：D

3．(2010·郑州二检)设a、b是两条直线，α、β是两个平面，则a⊥b的一个充分条件是

(　)

A．a⊥α，b∥β，α⊥β　

B．a⊥α，b⊥β，α∥β

C．a⊂α，b⊥β，α∥β　

D．a⊂α，b∥β，α⊥β

解析：依题意易知A，D中的位置关系不确定，故A、D错误；对于B，易知a∥b，故B错误；对于C，因为b⊥β，α∥β，故b⊥α，又a⊂α，所以a⊥b，故C正确．

答案：C

2．平面α⊥平面β的一个充分条件是

(　)

A．存在一条直线l，使得l⊥α，l⊥β

B．存在一个平面γ，使得γ⊥α，γ⊥β

C．存在一个平面γ，使得γ∥α，γ∥β

D．存在一条直线l，使得l⊥α，l∥β

解析：对于A，由l⊥α，l⊥β得α∥β，因此A不正确；对于B，若直线l⊥γ，则任意一个经过直线l的平面都与平面γ垂直，显然可以找到两个都经过直线l但互不垂直的平面α、β，因此B不正确；对于C，由γ∥α，γ∥β只能得出α∥β，因此C不正确；对于D，由l⊥α，l∥β可得α⊥β，因此D正确．

答案：D

1．过空间一点与已知平面垂直的直线有

(　)

A．0条　　　　　　　　　　　　　　　　 B．1条

C．0条或1条　 　　　　　　　　　　　　　　　　　　　　　　 D．无数条

解析：根据线面垂直的定义及其性质定理可知过空间一点与已知平面垂直的直线只有1条，故选B.

答案：B

22．(14分)(2010·北京东城模拟)甲、乙、丙三人进行某项比赛，每局有两人参加，没有平局，在一局比赛中，甲胜乙的概率为，甲胜丙的概率为，乙胜丙的概率为，比赛的规则是先由甲和乙进行第一局的比赛，然后每局的获胜者与未参加此局比赛的人进行下一局的比赛，在比赛中，有人获胜两局就算取得比赛的胜利，比赛结束．

(1)求只进行两局比赛，甲就取得胜利的概率；

(2)求只进行两局比赛，比赛就结束的概率；

(3)求甲取得比赛胜利的概率．

解：(1)只进行两局比赛，甲就取得胜利的概率为：

P₁＝×＝.

(2)只进行两局比赛，比赛就结束的概率为：

P₂＝×+×＝.

(3)甲取得比赛胜利共有三种情形：

若甲胜乙，甲胜丙，则概率为×＝；

若甲胜乙，甲负丙，丙负乙，甲胜乙，则概率为

×××＝；

若甲负乙，乙负丙，甲胜丙，甲胜乙，则概率为

×××＝.

所以，甲获胜的概率为++＝.

21．(12分)某部门组织甲、乙两人破译一个密码，每人能否破译该密码相互独立．已知甲、乙各自独立破译出该密码的概率分别为、.

(1)求他们恰有一人破译出该密码的概率；

(2)求他们破译出该密码的概率；

(3)现把乙调离，甲留下，并要求破译出该密码的概率不低于80%，那么至少需要再增添几个与甲水平相当的人？

解：记甲、乙破译出密码分别为事件A、B.则P(A)＝，P(B)＝.

(1)P(B+A)＝P()P(B)+P(A)P()＝×+×＝.

(2)他们破译出该密码的概率为：1－P()P()＝1－×＝.

(3)设共需要n个与甲水平相当的人，则应有1－()ⁿ≥80%，由此得()ⁿ≥5，所以n≥4.

故至少需要再增添3个与甲水平相当的人．