16．(2010·安徽巢湖一检)过点M(，1)的直线l与圆C：(x－1)²+y²＝4交于A、B两点，当∠ACB最小时，直线l的方程为__________．

解析：由平面几何知识可知，当l与CM垂直时∠ACB最小．

∵k_CM＝＝－2，

∴k_l＝，故直线l方程为y－1＝(x－)，即2x－4y+3＝0.

答案：2x－4y+3＝0

15．过点P(－3，－)且被圆x²+y²＝25所截得的弦长为8的直线方程为__________．

解析：由题意知，过P的直线y+＝k(x+3)⇒2kx－2y+6k－3＝0，圆心到直线的距离

d＝＝3⇒k＝－，验证知x＝－3满足条件．

故直线方程为3x+4y+15＝0或x＝－3.

答案：3x+4y+15＝0或x＝－3.

14．不等式组：表示的平面区域内的整点坐标为__________．

解析：如图3可知其整点坐标为

(－1，－1)．

答案：(－1，－1)

13．已知直线l₁：2x+m²y－2＝0，直线l₂：mx+2y－1＝0，若l₁⊥l₂，则m＝__________.

解析：由题意知m＝0时l₁⊥l₂，又因m≠0时，

(－)·()＝－1⇒m＝－1.

答案：0或－1

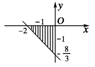
图3

12．已知向量m＝(a－2b，a)，n＝(a+2b,3b)，且m，n的夹角为钝角，则在平面aOb上，满足上述条件及a²+b²≤1的点(a，b)所在的区域面积S满足　　　　　　　　　　　　　 (　)

A．S＝π　 　　　　　　　　　　　　　　　　　　　　 B．S＝

C．S> 　　　　　　　　　　　　　　　　　　　　 D．S<

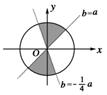
图2

解析：∵m，n的夹角为钝角，

∴cos〈m，n〉＝<0，

∴m·n<0，而

(a－2b，a)·(a+2b,3b)＝a²－4b²+3ab＝(a+4b)(a－b)<0.

∴或，

画出上述可行域及a²+b²≤1(如图2)．

显然直线b＝a与b＝－a的夹角为锐角．

∴S<.故应选D.

答案：D

11．已知三点A(－2,1)，B(－3，－2)，C(－1，－3)和动直线l：y＝kx，当点A、B、C到直线l的距离的平方和最小时，下列结论中正确的是　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．点A在l上　 　　　　　　　　　　　　　　　 B．点B在l上

C．点C在l上　 　　　　　　　　　　　　　　　 D．点A、B、C均不在l上

解析：点A、B、C到直线l的距离的平方和为：

d＝

＝14－.

要使d最小，显然k>0，

此时d＝14－≥14－7＝7.

当且仅当k＝，即k＝1时，等号成立．

所以，当k＝1时，d取最小值，此时点A、B、C均不在直线y＝x上．故选D.

答案：D

10．已知点M(0,1)、A(1,1)、B(0,2)，且＝cosθ+sinθ(θ∈[0，π])，则点P的轨迹方程是　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．x²+y²＝1(x≥0)

B．x²+y²＝1(y≥0)

C．x²+(y－1)²＝1(y≤1)

D．x²+(y－1)²＝1(y≥1)

解析：设P(x，y)，则＝(x，y－1)，

又＝(1,0)，＝(0,1)，故有(x，y－1)＝(cosθ，sinθ)，

∴x²+(y－1)²＝1.

又∵θ∈[0，π]，∴y＝sinθ+1≥1.∴选D.

答案：D

9．两圆相交于两点(1,3)和(m,1)，两圆的圆心都在直线x－y+＝0上，则m+c的值是

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．－1 　　　　　　　　　　　　　　　　　 B．2

C．3　 　　　　　　　　　　　　　　　　　　　 D．0

解析：由题意知两点(1,3)、(m,1)的中点(，2)在直线x－y+＝0上，即－2+＝0.∴m+c＝3.

答案：C

8．把直线x－2y+λ＝0向左平移1个单位，再向下平移2个单位后，所得直线正好与圆x²+y²+2x－4y＝0相切，则实数λ的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．3或13　 　　　　　　　　　　　　　　 B．－3或13

C．3或－13　 　　　　　　　　　　　　　 D．－3或－13

解析：直线x－2y+λ＝0按a＝(－1，－2)平移后的直线为x－2y+λ－3＝0，与圆相切，易得λ＝13或3.

答案：A

7．已知有向线段的起点P(－1,1)，终点Q(2,2)，若直线l：x+my+m＝0与有向线段的延长线相交，且过定点

M(0，－1)．如图1，则m的取值范围是　　　　　　　　　　　　　　　　　　 　　　　　　　　　　 (　)

图1

A．(，)

B．(－3，－)

C．(－∞，－3)

D．(－，+∞)

解析：易知k_PQ＝＝，

直线x+my+m＝0过点M(0，－1)．

当m＝0时，直线化为x＝0，一定与PQ相交，所以m≠0，

当m≠0时，k₁＝－，考虑直线l的两个极限位置．

(1)l经过Q，即直线l₁，则kl₁＝＝；

(2)l与平行，即直线l₂，则kl₂＝k_PQ＝，

所以<－<，

即－3<m<－.故选B.

答案：B