
4.在样本的频率分布直方图中,一共有m(m≥3)个小矩形,第3个小矩形的面积等于其余m-1个小矩形面积和的,且样本容量为100,则第3组的频数是
( )
A.0.2 B.25
C.20 D.以上都不正确
解析:第3组的频率是,样本容量为100,故第3组的频数是100×=20.选C.
答案:C
3.将容量为100的样本数据,按照从小到大的顺序分为8个组,如下表:
|
组号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
频数 |
x |
13 |
y |
14 |
z |
13 |
12 |
8 |
已知第1小组的频数是第3和第5小组的频数之和,第3小组的频率是第5小组的频率的三倍,则第3小组的频率为
( )
A.0.10 B.0.05
C.0.15 D.0.20
解析:根据题意,得
解得,所以第3组的频率为=0.15.
答案:C
2.采用简单随机抽样从个体数为6的总体中抽取一个容量为3的样本,则对于总体中指定的个体a前两次未被抽到,第三次恰好被抽到的概率为
( )
A. B.
C. D.
解析:解法1:对于从6个个体中抽取1个,每个个体被抽到的概率均为.
解法2:P==.
答案:A
1.某地区有300家商店,其中大型商店30家,中型商店75家,小型商店175家,为了掌握各商店的营业情况,要从中抽取一个容量为20的样本.若采用分层抽样的方法,抽到的中型商店数是
( )
A.2 B.3
C.5 D.13
解析:根据分层抽样按比例抽取,抽取的比例为=,抽取的中型商店数为75×=5.
答案:C
22.(14分)(2010·内蒙古赤峰统考)如图4,在平面直角坐标系中,N为圆A:(x+1)2+y2=16上的一点,点
B(1,0),点M是BN中点,点P在线段AN上,且·=0.
(1)求动点P的轨迹方程;
(2)试判断以PB为直径的圆与圆x2+y2=4的位置关系,并说明理由.
解:(1)由点M是BN中点,又·=0,可知PM垂直平分BN.
所以|PN|=|PB|,又|PA|+|PN|=|AN|,
所以|PA|+|PB|=4,|AB|=2.
由椭圆定义知,点P的轨迹是以A,B为焦点的椭圆.
设椭圆方程为+=1(a>b>0),
由2a=4,2c=2,可得a2=4,b2=3.
可知动点P的轨迹方程为+=1.
(2)设点P(x0,y0),PB的中点为Q,则Q(,),
|PB|==
==2-x0,
即以PB为直径的圆的圆心为Q(,),
半径为r1=1-x0,
又圆x2+y2=4的圆心为O(0,0),半径r2=2,
又|OQ|=
=
==1+x0,
故|OQ|=r2-r1,即两圆内切.
21.(12分)已知圆C的方程为x2+y2=4.
(1)直线l过点P(1,2),且与圆C交于A、B两点,若|AB|=2,求直线l的方程;
(2)圆C上一动点M(x0,y0),=(0,y0),若向量=+,求动点Q的轨迹方程,并说明轨迹是什么曲线.
解:(1)①若直线l垂直于x轴,则此直线为x=1,l与圆的两个交点坐标分别为(1,)和(1,-),这两点间的距离为2,符合题意.
②若直线l不垂直于x轴,设其方程为y-2=k(x-1)
即kx-y-k+2=0
设圆心到此直线的距离为d
∵2=2∴d=1
∴1=解得k=
故所求直线方程为3x-4y+5=0
综上所述所求直线方程是x=1或3x-4y+5=0.
(2)设Q点坐标为(x,y)
∵M点的坐标是(x0,y0),=(x0,y0),=(0,y0),
=+
∴(x,y)=(x0,2y0)∴
∵x+y=4∴x2+()2=4.即+=1,
∴Q点的轨迹方程是+=1.
Q点轨迹是一个焦点在y轴上的椭圆.
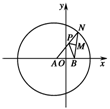
图4
20.(12分)圆C通过不同的三点P(k,0)、Q(2,0)、R(0,1),已知圆C在P点切线的斜率为1,试求圆C的方程.
解:设圆C的方程为x2+y2+Dx+Ey+F=0.
将P、Q、R的坐标代入,得
∴圆的方程为x2+y2-(k+2)x-(2k+1)y+2k=0,圆心为(,).
又∵kCP=-1,∴k=-3.
∴圆的方程为x2+y2+x+5y-6=0.
19.(12分)已知圆C的圆心在直线l1:x-y-1=0上,与直线l2:4x+3y+14=0相切,且截得直线l3:3x+4y+10=0所得弦长为6,求圆C的方程.
解:设圆心C(a,b),半径为r.
则a-b-1=0,r=,
=.
所以-=9.
即=9.
因为a-b=1,
所以=9,a+b=3.
由解之得
故所求圆C的方程为(x-2)2+(y-1)2=25.
18.(12分)已知直线l夹在两条直线l1:3x+y-2=0和l2:x+5y+10=0之间的线段被点D(2,-3)平分,求直线l的方程.
解:设l与l1交点为A(x1,y1),与l2交点为B(x2,y2),
∵D(2,-3)是AB中点,
∴=2,=-3.
因此
B(x2,y2)在l2上,得x2+5y2+10=0,
即4-x1+5(-6-y1)+10=0.
由此得解之得
∴A(,-),又直线l过A、D两点,
所以直线方程为=.
化为一般形式得l的方程为4x-y-11=0.
17.(12分)求与点P(4,3)的距离为5,且在两坐标轴的截距相等的直线方程.
解:设所求直线方程为y=kx或+=1(a≠0).
对于y=kx,
5=,9k2+24k+16=0,
解之得k=-.
对于x+y=a,5=,
解之得a=7+5或7-5.
故所求直线方程为
y=-x或x+y-7-5=0或x+y-7+5=0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com