11．2009年5月19日，中国平安集团旗下中国平安产险推出“平安甲型H1N1流感综合保险”，这是国内首款专门针对此次流感疫情设计开发的保险产品，主险责任涵盖由于甲型H1N1流感导致的身故和医疗费用，保障额度2万元至15万元不等。对此认识正确的是

(　)

①该保险具有行政性、强制性　②该保险属于财产保险　③订立该项保险合同时应遵循公平互利、协商一致、自愿订立的原则　④这有利于人民生活的稳定

A．①②　 　　　　　 B．②③

C．②④　 　　　　　 D．③④

[解析]　社会保险具有行政性、强制性的特点，该保险属于商业保险，①不选。该保险属于人身保险，②不选。

[答案]　D

10．2009年6月中旬，财政部下发了《中央财政森林保险保费补贴试点方案》，明确江西、福建、湖南作为2009年度中央财政森林保险保费试点省份。上述举措

(　)

A．可以为林业发展提供一定的保障

B．能够提高劳动者的工资收入

C．会避免林业灾害的发生

D．有助于调节货币的流通速度

[解析]　B、C、D是对农业保险保费补贴的误解。

[答案]　A

(2010年成都模拟)北京金隅集团有限责任公司发行总额80 000万元债券，期限10年，固定利率、票面利率4.43%。运用所学知识，完成8-9题。

8．该公司发行上述债券是为了

(　)

A．筹措短期资金、完善证券市场

B．筹措流动资金、解决经营困难

C．筹措长期资金、扩充生产设备

D．筹措财政资金、解决财政困难

[解析]　这种债券是公司债券，公司债券是为筹措长期资金、扩充生产设备而发行的。

[答案]　C

9．上述债券的特点是

(　)

A．安全系数较政府债券低，但比金融债券高

B．信用度高，代用率高，流通性强

C．安全系数较政府债券低，收益率低于金融债券

D．风险较高，但收益率往往也比较高

[解析]　公司债券的风险和收益均高于政府债券和金融债券。

[答案]　D

2009年5月当月居民存款增加1 886亿元，同比少增478亿元。据此回答6-7题。

6．居民存款的直接目的是

(　)

A．获得利息　 　　　　　　　 B．获得股息

C．支援现代化建设　 　　　　 D．成为银行股东

[解析]　注意“直接目的”关键词。

[答案]　A

7. 2009年5月份股市保持强劲涨势，居民投资意愿增强，股票和基金开户数都有所增加。居民户存款同比少增和近期股市的持续反弹有关。存款储蓄和投资股票的共同点是

(　)

A．都是有价证券

B．都是一种投资手段

C．前者是入股凭证，后者是债务凭证

D．既是投资行为，又是计划消费行为

[答案]　B

5．漫画中把存款转入炒股的人们

(　)

A．没有看到股市的高收益

B．没有意识到股市的高风险

C．选择了多种投资方式

D．没有看到股票和储蓄的性质不同

[解析]　A、C、D不符合漫画寓意。

[答案]　B

4．上述材料主要说明

(　)

A．居民储蓄，利国利民

B．储蓄是居民投资的最佳途径

C．我国资本市场发展的条件日益完善

D．居民储蓄和投资股市都可以获得收益

[解析]　居民投资的目的是获得收益，投资的途径有多种，是否最佳应看其收益率，故B不选。

[答案]　C

3．中国保持了较高的储蓄率，其根本原因是

(　)

A．我国投资渠道狭窄

B．我国人民养成了勤俭持家的良好习惯

C．我国居民收入大幅增加

D．我国国民经济保持快速增长

[解析]　注意关键词“根本原因”。

[答案]　D

2009年6月12日，中国人民银行公布的2009年第二季度全国城镇储户问卷调查结果显示，47%的城镇居民在安排支出时选择“更多地储蓄”，此比例比上季提高9.5个百分点，升至历史最高。据此回答1-2题。

1．　 居民储蓄意愿增强

2．　 (　)

①有利于银行吸纳社会资金　②表明居民注重计划消费　③表明受金融危机影响，人们的消费信心增强　④会进一步刺激消费，促进经济增长

A．①②　　　　B．②③

C．②④　 　　　　　 　D．③④

[解析]　居民储蓄意愿增强，表明消费信心不足，不利于刺激消费，拉动经济增长，③④不选。

[答案]　A

2．居民适量的存款储蓄

(　)

①可以为国家积累资金，支援现代化建设　②能有效调节市场货币流通　③有利于落实积极的财政政策　④是培养科学合理的消费习惯的根本途径

A．①②　 B．②③

C．②④　 D．③④

[解析]　储蓄和财政政策没有直接关系，③不选。④观点不正确。

[答案]　A

(2010年洛阳月考)随着国民经济快速增长，中国保持了较高的储蓄率，为加快资本市场发展提供了更为充分的中长期资金来源。同时，资本市场发展的外部环境得到明显改善，股改基本完成，金融机构市场退出机制和投资者保护制度逐渐完善，都为资本市场建设创造了有利条件。据此回3-4题。

2. 获得成功的体验和克服困难的经历。增强运用数学的信心．

教学重点

　　 探究“任意给定一个矩形，是否存在另一个矩形，它的周长和面积分别是已知矩形周

长和面积的一半”，从而获得解决问题的方法和途径．

教学难点

　　 从特殊到一般，启发学生综合运用一元二次方程、方程组、不等式等知识发现具有一般性的结论，寻求一般性的解决方法．

教学方法

　　 自主探索--合作交流．

教具准备

　　 多媒体演示

教学过程

　　 Ⅰ．创设情境问题，搭建探究平台

　　 [师]上一节课，我们研究了“任意给定一个矩形．一定存在另一个矩形，它的周长和面

积分别是已知矩形周长和面积的2倍”．如果我们把这个问题看成是“加倍”，那么“减半”如何呢？

　　 多媒体演示：

[问题]任意给定一个矩形．是否一定存在另一个矩形，它的周长和面积分别是已知矩形周长和面积的一半?你是怎么做的?

　　 [生]这个结论一定成立．

　　 [师]理由呢?

　　 [生]既然任意给定一个矩形，都存在一个新矩形，它的周长和面积分别是已知矩形周长和面积的2倍。也就是任何一个矩形的周长和面积可以同时“加倍”，那么原矩形自然满足新矩形的“减半”要求，即原矩形的周长和面积分别是新矩形周长和面积的一半．例如长和宽分别为3+ 和3-的矩形(记为A，其周长和面积分别是12和4)，是由长和宽分别为2和1的矩形(记为B)“加倍”而来的。因而矩形B的周长和面积分别是矩形A的周长和面积的一半．

　　 [师]你同意这位同学的观点吗？

　　 Ⅱ.展示思维过程，构建探索空间

　　 [师]请同学们结合上节课的内容，积极独立的思考.然后请大家在小组内研讨．

　　 [生]我不同意这位同学的观点．不是所有的矩形都可以“减半”，即不一定存在另一个矩形的周长和面积都为原矩形周长和面积的一半．他刚才举的只是一个特例．

　　 [师]你能简单扼要地说明你的理由吗?

　　 [生]可以上一节课我们在“做一做”中，先研究了一个简单的特殊的情形：如果已知矩形的长和宽分别为2和1，是否存在另一个矩形，它的周长和面积分别是已知矩形周长和面积的2倍?现在已无可质疑肯定存在．但我们在寻找这个矩形时还上费了一番周折的．先是固定所求矩形的周长：周长为12的矩形很多．它们的长和宽可以是5和1，4和2，3和3，和，…后又固定所求矩形的面积．面积为4的矩形也很多，它们的长和宽可以是4和1，2和2，和8，…但同时满足条件的只有一个，即长和宽分别为3+和3-.反过来长和宽分别为3+和3-的矩形一定存在另一个矩形.它的周长和面积都为原矩形的一半．即我们知道的长和宽分别为2和1的矩形．可是像上面的矩形长和宽分别为5和1.4和2，3和3，和，…；4和1，2和2，和8…，是否也存在一个矩形，它的周长和面积分别是上述矩形周长和面积的一半呢?我先考查了一下长和宽分别是5和1的矩形，看它是否能“减半”．

设“减半”后的矩形的长和宽分别为x．和y，则可得

x+y=3,

xy=,

如果此方程组有解．则说明这样的矩形存在；如果无解．则说明这样的矩形不存在．消去未知数y，可得x(3-x)= ,即x²-3x+=0，△＝(-3)²-4×1×＝9-10＝-1<0，所以方程组无解．由此可知不是所有的矩形都存在另一个矩形，它的周长和面积都是原矩形周长和面积的一半．

　　 [师]这位同学能独立思考，大胆地对问题提出质疑，表现很棒!下面我们再来看上节课研究过的几个特殊的矩形，看它们能否减半．

　　 多媒体演示：

做一做

如果已知矩形的长和宽仍为2和1，那么是否存在一个矩形。它的周长和面积分别是已知矩形周长和面积的一半?如果已知矩形的长和宽分别是3和1，4和1，6和1呢?

　　 [师]下面我们四人1组，分别考查已知矩形的长和宽为2和1，3和1.4和1，6和1的情形，然后我们将研究结果在全班交流．

[生]我们组考查的已知矩形的长和宽是2和1．设所求矩形的长和宽分别为x和y，

　 x+y=，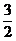

则　　　　　　

　　 xy=1，

消去y得．x(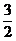-x)＝1，化简得，2x²-3x+2＝0,△＝9-16<0,所以方程组无解，即如果已知矩形的长和宽分别为2和1时，不存在一个矩形，它的周长和面积分别是已知矩形周长和面积的一半．

　　 [生]我们组考查的也是长和宽分别为2和1的矩形．但我们用的是函数图象的方法

考查,同上节课一样，我们把满足“减半”要求的矩形的长和宽设为x和y，则(x，y)可以看

作反比例函数y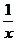＝的图象与一次函数y＝-x+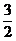的图象在第一象限内交点的坐标．从下图可以看到，这样的交点不存在，即满足要求的矩形不存在．

　　 [生]我们组用了同样的方法考查，发现已知矩形的长和宽为3和1时，“减半”的矩形也不存在．

　　 [生]已知矩形的长和宽分别为4和1时，“减半”的矩形也不存在．

[生]已知矩形的长和宽分别为6和1时，“减半”的矩形存在．我们设所求矩形的长和宽分别为x、y则

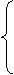x+y=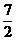

xy=3,

消去y化简得2x²-7x+6＝0.△=49-48＝1>0，∴x₁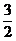＝，x₂＝2．即所求矩形的长和宽分别为2和．

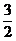　　 [师]我们可以发现当矩形的长和宽分别为n和1时，“减半”的矩形也可能存在，也可能不存在．请同学们思考一下，当已知矩形的长和宽分别为n和1时，满足什么条件，才存在新矩形，它的周长和面积分别是已知矩形周长和面积的一半呢?请同学们独立思考．

　　 [生]可以设所求矩形的长为x，则宽为[ (n+1)-x], x[ (n+1)-x]= n，化简得2x²-(n+1)x+n＝0．

　　 当△＝(n+1)²-8n＝n²+1-6n≥0时，方程有解，即符合条件的矩形存在．此时n²+1≥6n；当△＝n²+1-6n<0时，方程无解，即符合条件的矩形不存在，此时n²+1<6n．

　　 [师]同学们可将我们刚才讨论过的几个矩形的长和宽代入检验一下．

　　 [生]当已知矩形的长和宽分别为2和1时，n²+1＝2²+1＝5，6n=6×2＝12，5<12，所以不存在一个矩形，它的周长和面积分别是已知矩形的周长和面积的一半．

　　 [生]当已知矩形的长和宽分别为3和1，4和1,5和1时，分别代入n²+1和6n中，都得到n²+1<6n，因此它们都不存在“减半”后的矩形．但当已知矩形的长和宽分别为6和1，n²+1＝6²+1=37,6n＝6×6＝36，37＞36．即n²+1>6n，所以存在“减半”后的矩形．

　　 [师]你能对更一般的情况研讨吗?

　　 多媒体演示：

议一议

当矩形满足什么条件时，才存在一个新的矩形，它的周长和面积分别是已知矩形周长和面积的一半?你能再找一个这样的例子吗?

　　 (教学时，可依据实际情况对不同学生提出不同的要求，不必要求所有学生都能进行严格、准确的数学表述)

　 　[生]可以设已知矩形的长和宽分别为

n，m，所求矩形的长为x，宽为[(m+n)-x]，那么x[(m+n)-x]＝mn，化简，得2x²-(m+n)x+mn＝0．①

　　 (1)当△＝(m+n)²-4×2mn＝m²+n²-6mn≥0，即m²+n²≥6mn时，方程①有解所以当已知矩形的长和宽为m和n时．如果m²+n²≥6mn，则存在一个新矩形，它的周长和面积分别是已知矩形周长和面积的一半．

　　 (2)当△＝(m+n)²-4×2mn＝m²+n²-6mn<0．即m²+n²<6mn时，方程①无解，所以当已知矩形的长和宽为m和n时，如果m²+n²<6mn，则存在一个新矩形．它的周长和面积分别是已知矩形周长和面积的一半．

　　 [师]你能找到一个已知矩形．存在一个新矩形，它的周长和面积分别是已知矩形周长和面积的一半吗?

　　 [生]可设已知矩形的长和宽分别为8和1，因为8²+1²＝65，6×8×1=48，65＞48，所

以这个矩形存在一个新矩形，它的周长和面积分别是已知矩形周长和面积的一半．

　　 [生]我也可以举一个例子，如果已知矩形的长和宽分别为12和2，而12²+2²＝148，6×12×2＝144，148>144，所以这个矩形也存在一个新矩形，它的周长和面积分别是已知矩形周长和面积的一半．

　　 [师]还能举一个“不存在”的情况吗?

　　 [生]例如：已知矩形的长和宽分别为10和2，因为10²+2²=104,6×10×2=120，104＜120，所以，不存在一个新的矩形，它的周长和面积分别是已知矩形周长和面积的一半．

　 　Ⅲ．课时小结

　　 本节课又一次为学生提供了一个思考、探究的平台，在活动中，同学们能积极参与数学活动，独立思考问题，体现归纳、综合和拓展的能力，感悟处理问题的策略和方法，积累了数学活动经验．获得了成功的体验．

　 　Ⅳ．课后作业

　　 习题P₁₅₃第2、4题．

　 　Ⅴ．活动与探究

　　 借助函数图象，探讨以下问题：对面积为1的矩形来说，它的周长最小是多少--凡是周长要求小于这个值的矩形都是不存在的；或者，对周长为3的矩形来说，它的面积最大是多少--凡是面积要求大于这个值的矩形也都是不存在的．

[过程]我们设面积为1的矩形的长和宽为x和y，则xy＝1．反比例函数y=在第一象限内的图象上的点的坐标(x，y)都可以作为面积为1的矩形的长和宽．设此矩形的周长为2a，则x+y＝a，满足要求x+y＝a的(x，y)可看作一次函数y＝-x+a的图象在第一象限内的点的坐标．这样的点有无数多个．但对面积为1的矩形来说，它的周长最小，即2a最小也就是a最小，那么满足条件的(x，y)既在y＝上，也在y＝-x+a上，并且要求直线y=-x+a与x轴或y轴的交点(a，0)或(0，a)中a的值必须最小(如下图所示)．

　　 由上图可知符合要求的只有l₁，此时a=2，周长的最小值为2a＝4．而当a<2时，如直线l₂，说明周长小于4而面积为1的矩形不存在；而当a>2时，如直线l₃、l₄，说明周长大于4而面积小于1的矩形有无数多个．

同理可以讨论周长为3的矩形，它的面积最大是多少,设此矩形的长和宽为x和y，则2(x+y)＝3，x+y=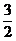；xy＝S．(如下图所示)

　　 由图可知，对周长为3的矩形来说，它的面积的最大值是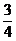×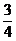=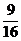,凡面积要求大于这个值的矩形不存在，而面积小于这个值的矩形有无数个．

　　 [结果]当矩形的面积一定时，周长有最小值．当矩形的周长一定时，面积有最大值．

板书设计

　　 课题学习--猜想、证明、拓广(二)

[问题]任意给定一个矩形，是否一定存在另一个矩形，它的周长和面积分别是已知矩形周长和面积的一半?

　　 从特殊到一般：

　　 (1)考查已知矩形的长和宽仍为2和1，3和1，4和1，5和1．6和1的情况．

　　 (2)考查已知矩形的长和宽为n和1的情况．

　　 当n²+1≥6n时，存在新矩形满足条件；

　　 当n²+1<6n时，不存在新矩形满足条件．

　　 (3)考查已知矩形的长和宽为m和n的情况．

　　 当m²+n²≥6mn时，存在新矩形满足条件；

　　 当m²+n²<6mn时，不存在新矩形满足条件．

1．积极参与数学活动，积极思考并与同学合作交流．