
1. 了解导数的概念,初步会用定义式解决一些问题;
[例1]求下列函数的导数:
(1)y=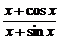
 (2)y=ln(x+
(2)y=ln(x+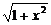 );
);
(3)y=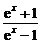 ;
;
解: (1)y′=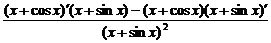
=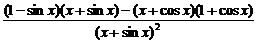
=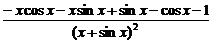
(2)y′=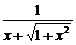 ·(x+
·(x+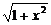 )′
)′
=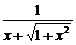 (1+
(1+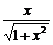 )=
)=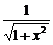
(3)y′=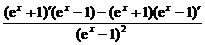 =
=
◆提炼方法:题(1)是导数的四则运算法则;題(2)(3)是复合函数的求导方法.都是导数问题的基础.
[例2](1)求曲线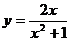 在点(1,1)处的切线方程;
在点(1,1)处的切线方程;
(2)运动曲线方程为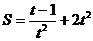 ,求t=3时的速度
,求t=3时的速度
分析:根据导数的几何意义及导数的物理意义可知,函数y=f(x)在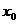 处的导数就是曲线y=f(x)在点
处的导数就是曲线y=f(x)在点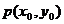 处的切线的斜率
处的切线的斜率 瞬时速度是位移函数S(t)对时间的导数
瞬时速度是位移函数S(t)对时间的导数
解:(1)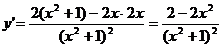 ,
,
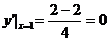 ,即曲线在点(1,1)处的切线斜率k=0
,即曲线在点(1,1)处的切线斜率k=0
因此曲线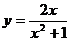 在(1,1)处的切线方程为y=1
在(1,1)处的切线方程为y=1
(2)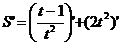
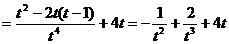
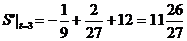
解题点评:切线是导数的“几何形象”,是函数单调性的“几何”解释,要熟练掌握求切线方程的方法.
[例3]若f(x)在R上可导,(1)求f(-x)在x=a处的导数与f(x)在x=-a处的导数的关系;(2)证明:若f(x)为偶函数,则f′(x)为奇函数.
分析:(1)需求f(-x)在x=a处的导数与f(x)在x=-a处的导数;(2)求f′(x),然后判断其奇偶性.
(1)解:设f(-x)=g(x),则
g′(a)=

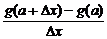
=
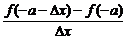
=-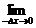
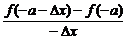 =-f′(-a)
=-f′(-a)
∴f(-x)在x=a处的导数与f(x)在x=-a处的导数互为相反数.
(2)证明:f′(-x)=

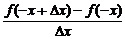
=
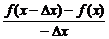
=-
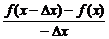 =-f′(x)
=-f′(x)
∴f′(x)为奇函数.
解题点注:用导数的定义求导数时,要注意Δy中自变量的变化量应与Δx一致.
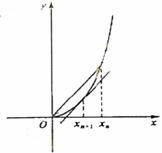
[例4](2006浙江)已知函数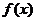 =x3+x2,数列 { xn } (xn > 0)的第一项x1=1,以后各项按如下方式取定:曲线y=
=x3+x2,数列 { xn } (xn > 0)的第一项x1=1,以后各项按如下方式取定:曲线y=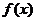 在
在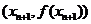 处的切线与经过(0,0)和(xn,f(xn))两点的直线平行(如图)。求证:当n
处的切线与经过(0,0)和(xn,f(xn))两点的直线平行(如图)。求证:当n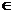
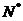 时:
时:
(I)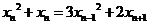 ;(II)
;(II)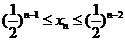
证明:(I)∵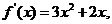
∴曲线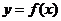 在
在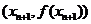 处的切线斜率
处的切线斜率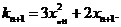
∵过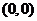 和
和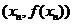 两点的直线斜率是
两点的直线斜率是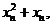
∴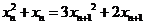 .
.
(II)∵函数 当
当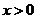 时单调递增,
时单调递增,
而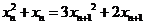
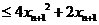
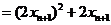 ,
,
∴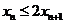 ,即
,即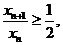
因此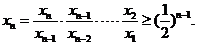
又∵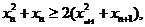
令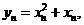 则
则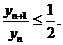
∵ ∴
∴
因此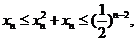 故
故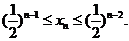
考查知识:函数的导数、数列、不等式等基础知识,以及不等式的证明,同时考查逻辑推理能力。
7. (1,e) e; 8. 2n+1-2.
6. 答案: -. 依题意
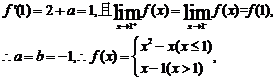
作图易得函数的最小值是f()=-
8.对正整数n,设曲线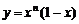 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为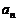 ,则数列
,则数列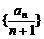 的前n项和的公式是
的前n项和的公式是
简答:1-4.CDCC; 5. ;
7.(2005北京)过原点作曲线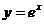 的切线,则切点的坐标为
,切线的斜率为 .
的切线,则切点的坐标为
,切线的斜率为 .
6.设函数 若该函数在实数集R上可导,则该函数的最小值是____.
若该函数在实数集R上可导,则该函数的最小值是____.
5. (2006全国Ⅰ)设函数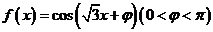
 若
若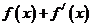 是奇函数,则
是奇函数,则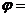 __________
__________
4.(2006湖南)设函数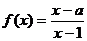 , 集合
, 集合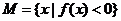 ,
,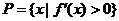 若
若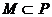 , 则实数
, 则实数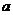 的取值范围是 ( )
的取值范围是 ( )
A.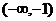 B.
B.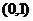 C.
C.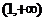 D.
D.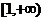
3.(2005湖南)设f0(x) = sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x) = fn′(x),n∈N,则f2005(x)= ( )
A.sinx B.-sinx C.cosx D.-cosx
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com