练习册

  • 练习册
  • 试题
     0  375865  375873  375879  375883  375889  375891  375895  375901  375903  375909  375915  375919  375921  375925  375931  375933  375939  375943  375945  375949  375951  375955  375957  375959  375960  375961  375963  375964  375965  375967  375969  375973  375975  375979  375981  375985  375991  375993  375999  376003  376005  376009  376015  376021  376023  376029  376033  376035  376041  376045  376051  376059  447090 
    1. ignore / neglect / overlook
    [解释]
    ignore　　 通常指有意不顾，或不理会显而易见的事物。
    neglect　 侧重指有意的忽略或忽视，也可指粗心与疏忽。
    overlook　 指因匆忙而疏忽或视而不见。
    　[练习]用上面所提供的辨析词的适当形式填空
    1We could not afford to _________ such a serious offence.
    2). He utterly ________ my warnings and met with an accident.
    3). Don’t ________ paying him a visit now and then.
    答案:　 　　　 1). overlooked　　　　　　 2). ignored　 　　　　　　　 3). neglect
    2. cheat / fool
    [解释]
    cheat　 主要指盈利的买卖中或游戏竞赛中欺骗人，骗取人的钱等。
    fool　 “愚弄”，指利用人缺乏常识，心理脆弱来欺骗人。
    [练习]用上面所提供的辨析词的适当形式填空
    1). You may get _________ in that shop.
    2). He can’t __________ her. She sees through him every time.
    答案:　 1). cheated　 2). fool
    3. calm / quiet / silent / still
    [解释]
    calm　　 天气、水、水面(表风平浪静)；(指人时)表示镇定自如。
    quiet　　 表“宁静”、“安静”、“寂静”，侧重没有响声，没有噪音和没有动静。指人时侧重性格温和，文静。
    silent　 表“沉默”、“不发言”、“不说话”，常常表示人不爱说话，沉默无语。
    still　 “不动的”，指人时侧重一动不动，；指物时指完全没有声音，突出静止不动。
    [练习]用上面所提供的辨析词的适当形式填空
    1). Please stand __________ while I take your photo.
    2). Why do you keep __________?
    3). Everything was ___________.
    4). He remained ___________ in the face of the enemy.
    答案: 1). still　　　　　　 2). silent　　　　　　　 3). quiet　　　　 4). calm
    4. join / join in / take part in / attend
    [解释]
    join　　　 　 表示参加组织、党派、团体、军队、俱乐部等
    join in　 　 表示参加游戏、活动等；join sb. (in sth.) 表(和某人一起)做某事
    take part in表示参与、参加讨论、游行、比赛、战斗、斗争、运动、庆祝等
    attend　 　 主要指出席、参加会议、婚礼；听讲座、课、报告、音乐会等；上学、教堂
    [练习]用上面所提供的辨析词的适当形式填空
    1). Can I ___________ the game?
    2). Did you ____________ the fighting?
    3). He __________ the army last year.
    4). A lot of people __________ her wedding.
    答案: 1). join in 2). take part in　　　　　　 3). joined　　　 　 4)attended

    试题详情

    例1x,y是满足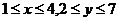的整数，则以(x,y)为坐标的点有多少个

    　 当x=1,2时y=2,3,4,5,6,7　 当x=3，，时，y=3，4，5，6，7，当x=4时，y=4，5，6，7，故共有21个

    变式设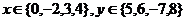，则以(x,y)为坐标的点，在第一象限的有___6__个，在第二象限的点有__3____个，在坐标轴上的有__4____个

    例2.　 从集合{1，2，3，…，10}中，选出由5个数组成的子集，使得这5个数中的任何两个数的和不等于11，这样的子集共有多少个?

    因为1+10=2+9=3+8=4+7=5+6=11,故共有个

    变题：上例中选出5个数组成子集改为选出4个数呢?　 5=80

    例3.某城市在中心广场建造一个花圃，花圃分为6个部分(如下图).现要栽种4种不同颜色的花，每部分栽种一种且相邻部分不能栽种同样颜色的花，不同的栽种方法有____120_________种.(以数字作答)

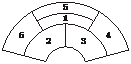
    例4.　 关于正整数2160，求它有多少个不同的正因数？40

    例5 若把两条异面直线看成“一对”，则六棱锥的棱所在的12条直线中，异面直线共有____24______对

    例6有红.黄，蓝旗各3面，每次升一面，二面，三面在某一旗杆上纵向排列，表示不同的信号，顺序不同则表示不同的信号，共可以组成多少种不同的信号　　 3+9+27=39

    同步练习

    1如图，一环形花坛分成四块，现有4种不同的花供选种，要求在每块里种1种花，且相邻的2块种不同的花，则不同的种法总数为(　 B )A．96　　 B．84　 C．60　 D．48　　　　　　　

    2 从正方体的6个面中选取3个面，其中有2个面不相邻的选法共有

    A.8种　　　　　　　 B.12种　　　　　　　 C.16种　　　　　　　 D.20种

    3 有三个不同的信箱，今有四封不同的信欲投其中，则不同的投法有　　　 种。

    A．81　　　　　　　 B．64　　　　　　　 C．24　　　　　　　 D．4

    4如图一,要给①,②,③,④四块区域分别涂上五种颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,则不同涂色方法种数为() A. 180　　 B. 160　　 C. 96　　 D. 60

    　

    若变为图二为____240_____种,图三为____320______种

    5 设直线的方程是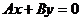，从1，2，3，4，5这五个数中每次取两个

    不同的数作为A、 B的值，则所得不同直线的条数是(　 )

    　A．20　　　　　　 B．19　　　　　　 C．18　　　　　　 D．16

    6将1，2，3填入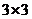的方格中，要求每行、每列都没有重复数字，右面是一种填法，则不同的填写方法共有(　　 )A．6种　　　 B．12种　　 C．24种　　 D．48种

    7 某通讯公司推出一组手机卡号码，卡号的前七位数字固定，从“×××××××0000”到“×××××××9999”共10000个号码.公司规定：凡卡号的后四位带有数字“4”或“7”的一律作为“优惠卡”，则这组号码中“优惠卡”的个数为(　 　)

    A.2000　　　 B.4096　　　 C.5904　　　 D.8320

    8从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种，分别种在不同土质的三块土地上，其中黄瓜必须种植，不同的种植方法共有(　　 )A．24种　 　B．18种　 　C．12种　 D．6种

    9在1，2，3，4，5这五个数字组成的没有重复数字的三位数中，各位数字之和为偶数的共有(　 )

    (A)36个　 (B)24个　 (C)18个　 　 (D)6个

    10 从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同工作．若其中甲、乙两名支援者都不能从事翻译工作，则选派方案共有(　 )(A)280种　 (B)240种　 (C)180种　　 (D)96种

    11从1，3，5，7中任取2个数字，从0，2，4，6，8中任取2个数字，组成没有重复数字的四位数，其中能被5整除的四位数共有　　 300 　　个。(用数字作答)

    12用1，2，3，4，5，6组成六位数(没有重复数字)，要求任何相邻两个数字的奇偶性不同，且1和2相邻，这样的六位数的个数是　 　40 　　

    13如图，A、B、C、D是海上的四个小岛，要建三座桥，将这四个岛连接起来，不同的建桥方案共有　　 16　 　　　种.

    　 14 将3种作物种植在如图5块试验田里，每块种植一种作物且相邻的试验田不能种植同一作物，不同的种植方法共有　 42　 　　　种

    15将数字1，2，3，4，5，6拼成一列，记第个数为，若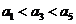，，，，则不同的排列方法种数为________种30

    试题详情

    　分类计数原理和分步计数原理

    (1)分类计数原理(加法原理)：

    做一件事情，完成它可以有n类办法，在第一类办法中有m1种不同的方法，在第二类办法中有m2种不同的方法，……，在第n类办法中有mn种不同的方法。那么完成这件事共有　 N=m1+m2+…+mn 种不同的方法。

    (2) 分步计数原理(乘法原理)：

    做一件事情，完成它需要分成n个步骤，做第一步有m1种不同的方法，做第二步有m2种不同的方法，……，做第n步有mn种不同的方法，那么完成这件事有 N=m1×m2×…×mn　

    种不同的方法。

    二基础练习

    1 十字路口来往的车辆，如果不允许回头，则行车路线共有　 (　 ).

    A.24种　 　　　　 B.16种　 　　　　 C.12种　 　　　 D.10种

    2 5名运动员争夺3项比赛冠军(每项比赛无并列冠军)，那么获得冠军的可能种数为( )A、125　　　　　 B、243　　 C、60　　　　　 D、10

    3 某城市的电话号码，由七位升为八位(首位数字均不为零)，则该城市可增加的电话部数是　 (　 )

    A.9×8×7×6×5×4×3×2　 B.8×97　 C.9×107 D.81×106

    4.72的正约数共有____12______个.

    5 从－1，0，1，2这四个数中选三个不同的数作为函数f(x)=ax2+bx+c的系数，可组成不同的二次函数共有___18_________个，其中不同的偶函数共有______6______个.(用数字作答)

    试题详情


    同步练习册答案