
1.由

4. 从数据中去寻找
根据计算或题给信息,可获取某些数据,这些数据也可使我们找到突破口。如物质的熔点较低,说明为分子晶体;反之,则可为离子晶体或原子晶体。
3. 从典型性质寻找
(1)同一元素的气态氢化物和气态氧化物反应,生成该元素的单质和水,元素可能是硫或氮。(2)同一元素的气态氢化物和最高价氧化物对应的水化物化合,生成盐的元素一定是氮。(3)两溶液混合生成沉淀和气体,这两种溶液的溶质可能分别是a.Ba(OH)2与(NH4)2SO4,b.可溶性铝盐与可溶性金属硫化物或可溶性碳酸盐或碳酸氢盐,c.可溶性铁盐与可溶性碳酸盐或碳酸氢盐,d.硫代硫酸盐与强酸(如盐酸、稀H2SO4等)。(4)既能与酸反应,又能与碱反应的物质可能是Al、Al2O3、Al(OH)3、氨基酸,弱酸的铵盐、弱酸的酸式盐等。(5)既能与强酸反应放出气体又能与强碱反应放出气体,常见的物质有:Al,弱酸的铵盐((NH4)2CO3、NH4HCO3、(NH4)2SO3、(NH4)2S、NH4HS等)。(6)在水中分解生成气体和难溶物或微溶物的物质可能是Al2S3、Mg3N2、CaC2等。(7)与水接触放出气体的常见物质有:Li、Na、K、Na2O2、F2等。(8)A物质加到B物质中,先生成沉淀,后沉淀又溶解,A、B可能分别是CO2与Ca(OH)2、NaOH与铝盐、NH3与AgNO3、HCl与NaAlO2、稀盐酸与Fe(OH)3 胶体等。
(9)使溴水褪色的物质有H2S、SO2、不饱和烃类、活泼金属、碱类等。
2. 从反应类型寻找
例如,同一元素的气态氢化物和气态氧化物反应生成该元素的单质和水,则该元素可能为S或N;两种溶液混合生成沉淀和气体,则反应可能为Ba(OH)2与(NH4)2SO4,或可溶性铝盐、可溶性铁盐与可溶性金属硫化物(如Na2S、NaHS)、可溶性碳酸盐、可溶性亚硫酸盐之间的双水解反应;遇水能分解成气体和难溶性物质的可能为Al2S3或Mg3N2;能“三合一”的反应有:NH3+H2O+CO2=NH4HCO3;
4Fe(OH)2+2H2O+O2=4Fe(OH)3;
4NO2+O2+2H2O=4HNO3。常见的一种物质能分解生成三种物质的反应,该物质可能为硝酸盐或NH4HCO3。电解某种盐溶液,能生成一种金属,放出一种气体及另一种物质,则该盐为不活泼金属的含氧酸盐,可为CuSO4、AgNO3等;如有物质发生下列转化关系:A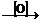 B
B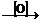 C,则必须对所学基础知识进行全面的总结与梳理,做到胸中有知识网络。如A为无机物单质,则可为C、S、N、Na等;如A为有机物,则可为乙烯或醇类,等等。
C,则必须对所学基础知识进行全面的总结与梳理,做到胸中有知识网络。如A为无机物单质,则可为C、S、N、Na等;如A为有机物,则可为乙烯或醇类,等等。
1. 从物质的组成、结构方面寻找
例如,具有正四面体结构的物质可能为甲烷或白磷或NH4+;不含金属元素的离子化合物为铵盐;组成为A2B2型的物质可能为Na2O2、H2O2、C2H2等。
3.应根据定义找两个向量的夹角。对于不共起点的两个向量,通过平移,使起点重合.
2.注意 ·
· 与ab的区别.
与ab的区别. ·
· =0≠>
=0≠> =
= ,或
,或 =
= .
.
1.运用向量的数量积可以解决有关长度、角度等问题.因此充分挖掘题目所包含的几何意义,往往能得出巧妙的解法.
5.向量数量积的运算律:
⑴  ·
· = ;
= ;
⑵ (λ )·
)· = =
= = ·(λ
·(λ )
)
⑶ ( +
+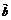 )·
)·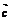 =
=
|
例1. 已知| |=4,|
|=4,| |=5,且
|=5,且 与
与 的夹角为60°,求:(2
的夹角为60°,求:(2 +3
+3 )·(3
)·(3 -2
-2 ).
).
解:(2 +3
+3 )(3
)(3 -2
-2 )=-4
)=-4
变式训练1.已知| |=3,|
|=3,| |=4,|
|=4,| +
+ |=5,求|2
|=5,求|2 -3
-3 |的值.
|的值.
解:
例2. 已知向量 =(sin
=(sin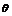 ,1),
,1), =(1,cos
=(1,cos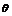 ),-
),- .
.
(1) 若a⊥b,求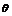 ;
;
(2) 求| +
+ |的最大值.
|的最大值.
解:(1)若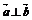 ,则
,则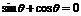
即 而
而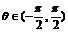 ,所以
,所以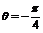
(2)
当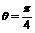 时,
时,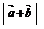 的最大值为
的最大值为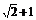
变式训练2:已知 ,
, ,其中
,其中 .
(1)求证:
.
(1)求证: 与
与 互相垂直;
(2)若
互相垂直;
(2)若
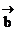 与
与
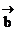 的长度相等,求
的长度相等,求 的值(
的值(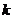 为非零的常数).
为非零的常数).
证明: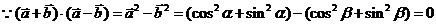
 与
与 互相垂直
互相垂直
(2)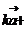
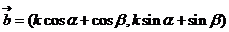 ,
,

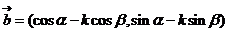 ,
,
 ,
,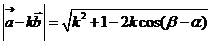 ,
,
而
 ,
,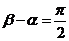
例3. 已知O是△ABC所在平面内一点,且满足( -
- )·(
)·( +
+ -2
-2 )=0,判断△ABC是哪类三角形.
)=0,判断△ABC是哪类三角形.
解:设BC的中点为D,则( )(
)( )=0
)=0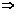 2
2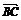 ·
· =0
=0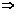 BC⊥AD
BC⊥AD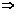 △ABC是等腰三角形.
△ABC是等腰三角形.
变式训练3:若 ,则△ABC的形状是
.
,则△ABC的形状是
.
解: 直角三角形.提示:
例4. 已知向量 =(cosθ, sinθ)和
=(cosθ, sinθ)和 =(
=( -sinθ, cosθ) θ∈(π, 2π)且|
-sinθ, cosθ) θ∈(π, 2π)且|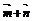 |=
|=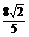 ,求cos(
,求cos(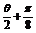 )的值.
)的值.
解: =(cosθ-sinθ+
=(cosθ-sinθ+ , cosθ+sinθ)由已知(cosθ-sinθ+
, cosθ+sinθ)由已知(cosθ-sinθ+ )2+(cosθ+sinθ)2=
)2+(cosθ+sinθ)2=
化简:cos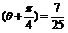
又cos2
∵θ∈(π,
2π) ∴cos <0
<0
∴cos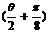 =-
=-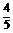
变式训练4.平面向量 ,若存在不同时为
,若存在不同时为 的实数
的实数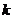 和
和 ,使
,使 ,
,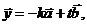 且
且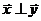 ,试求函数关系式
,试求函数关系式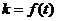 .
.
解:由 得
得
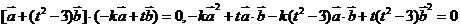
|
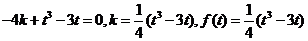
4.向量数量积的性质:设 、
、 都是非零向量,
都是非零向量, 是单位向量,θ是
是单位向量,θ是 与
与 的夹角.
的夹角.
⑴  ·
· =
= ·
· =
=
⑵  ⊥
⊥
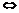
⑶ 当 与
与 同向时,
同向时, ·
· = ;当
= ;当 与
与 反向时,
反向时, ·
· = .
= .
⑷ cosθ= .
⑸ | ·
· |≤
|≤
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com