1．(2009·四川高考)已知函数f(x)＝sin(x－)(x∈R)，下面结论错误的是

(　)

A．函数f(x)的最小正周期为2π

B．函数f(x)在区间[0，]上是增函数

C．函数f(x)的图象关于直线x＝0对称

D．函数f(x)是奇函数

解析：∵f(x)＝sin(x－)＝－cosx(x∈R)，∴函数f(x)是最小正周期为2π的偶函数，故选D.

答案：D

13．(20分)(2009·重庆高考)设函数f(x)＝sin－2cos²x+1.

(1)求f(x)的最小正周期；

(2)若函数y＝g(x)与y＝f(x)的图象关于直线x＝1对称，求当x∈时，y＝g(x)的最大值．

解：(1)f(x)＝sinxcos－cosxsin－cosx

＝sinx－cosx＝sin，

故f(x)的最小正周期为T＝＝8.

(2)解法1：在y＝g(x)的图象上任取一点(x，g(x))，它关于x＝1的对称点为(2－x，g(x))．

由题设条件，点(2－x，g(x))在y＝f(x)的图象上，从而

g(x)＝f(2－x)＝sin

＝sin＝cos.

当0≤x≤时，≤x+≤，因此y＝g(x)在区间上的最大值为g(x)_max＝cos＝.

解法2：因区间关于x＝1的对称区间为，且y＝g(x)与y＝f(x)的图象关于x＝1对称，故y＝g(x)在上的最大值即为y＝f(x)在上的最大值．

由(1)知f(x)＝sin，

当≤x≤2时，－≤x－≤.

因此y＝g(x)在上的最大值为

g(x)_max＝sin＝.

12．(15分)(2009·天津重点学校联考)已知函数f(x)＝sin²x+sinxcosx+2cos²x，x∈R.

(1)求函数f(x)的最小正周期；

(2)将函数f(x)的图象按向量a＝(，－)平移后得到函数g(x)的图象，求g(x)的解析式；

(3)在给定的坐标系中(如图6)画出函数y＝g(x)在区间[0，π]上的图象．

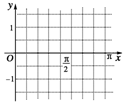
图6

解：(1)f(x)＝+sin2x+(1+cos2x)

＝sin2x+cos2x+＝sin(2x+)+.

∴f(x)的最小正周期T＝＝π.

(2)把f(x)图象上所有的点按向量a＝(，－)平移后，所得到的图象的解析式为

g(x)＝sin[2(x－)+]+－

＝sin(2x－)．

(3)由y＝sin(2x－)，知

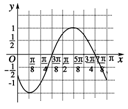
图7

11．(15分)函数f₁(x)＝Asin(ωx+φ)(A>0，ω>0，|φ|<)的一段图象过点(0,1)，如图5所示．

(1)求函数f₁(x)的表达式；

(2)将函数y＝f₁(x)的图象向右平移个单位，得函数y＝f₂(x)的图象，求y＝f₂(x)的最大值，并求出此时自变量x的集合．

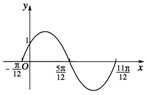
图5

解：(1)由图知，T＝π，于是ω＝＝2.

将y＝Asin2x的图象向左平移，

得y＝Asin(2x+φ)的图象，

于是φ＝2·＝.

将(0,1)代入y＝Asin(2x+)，得A＝2.

故f₁(x)＝2sin(2x+)．

(2)依题意，f₂(x)＝2sin[2(x－)+]

＝－2cos(2x+)，

当2x+＝2kπ+π，

即x＝kπ+(k∈Z)时，y_max＝2.

x的取值集合为{x|x＝kπ+，k∈Z}．

10．(2009·福建师大附中模拟)下列命题：

①函数y＝sinx在第一象限是增函数；

②函数y＝|cosx+|的最小正周期是π；

③函数y＝tan的图象的对称中心是(kπ，0)，k∈Z；

④函数y＝lg(1+2cos2x)的递减区间是[kπ，kπ+)，k∈Z；

⑤函数y＝3sin(2x+)的图象可由函数y＝3sin2x的图象按向量a＝(，0)平移得到．

其中正确的命题序号是__________．

答案：③④

9．设函数f(x)＝sin2x，若f(x+t)是偶函数，则t的一个可能值是__________．

解析：∵f(x+t)＝sin2(x+t)＝sin(2x+2t)是偶函数，

∴f(x+t)＝f(－x+t)，

即sin(2x+2t)＝sin(－2x+2t)．

∴2x+2t＝－2x+2t+2kπ，k∈Z，

或2x+2t＝π－(－2x+2t)+2kπ，k∈Z.

∴t＝π，k∈Z.

答案：，，，…，π(k∈Z)

8．将函数y＝f(x)·sinx(x∈R)的图象向右平移个单位后，再作关于x轴对称变换，得到函数y＝1－2sin²x的图象，则f(x)可以是________．

解析：将y＝f(x)sinx的图象向右平移个单位得

y＝f(x－)sin(x－)的图象，

其关于x轴的对称图象的解析式为

y＝－f(x－)sin(x－)，

∵y＝1－2sin²x＝cos2x＝sin(－2x)

＝2sin(－x)cos(－x)＝－2cos(x－)sin(x－)

∴f(x－)＝2cos(x－)，故f(x)＝2cosx.

答案：2cosx

7．(2009·江苏高考)函数y＝Asin(ωx+φ)(A，ω，φ为常数，A>0，ω>0)在闭区间

　[－π，0]上的图象如图4所示，则ω＝______.

图4

解析：由题图可知，T＝，　 　　　　　　　　　　　　　　

∴ω＝＝3.

答案：3

6．(2009·浙江高考)已知a是实数，则函数f(x)＝1+asinax的图象不可能是

(　)

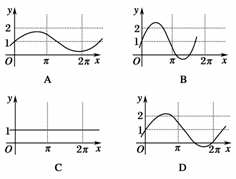
解析：当a＝0时f(x)＝1，C符合，

当0<|a|<1时T>2π，A符合，

当|a|>1时T<2π，B符合．排除A、B、C，故选D.

答案：D

5．方程2sin2x＝x－3的解有

(　)

A．1个　　　　　　 B．2个

C．3个　 　　　　　　　　　　　　　　　　　 D．4个

解析：作y＝sin2x与y＝的图象可得其交点为3个且在x∈(0,2π)上．故选C.

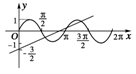
图3

答案：C