8．若θ角的终边与的终边相同，则在[0,2π]内终边与角的终边相同的角是________．

解析：由已知θ＝2kπ+(k∈Z)，

∴＝+(k∈Z)，

由0≤+≤2π，得－≤k≤，

∵k∈Z，∴k＝0,1,2,3，

∴依次为π，π，π，π.　 　　　　　　　　　　　　　　

答案：π，π，π，π

7．一个扇形的面积为4 cm²，周长为8 cm，则扇形的圆心角及相应的弦长分别是__________．

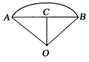
图2

解析：如图2所示，设扇形的半径为R，圆心角为α，则有

解得

取AB的中点C，连OC，则OC⊥AB，

且∠AOC＝＝1.∴AB＝2Rsin＝4sin1.

故所求的圆心角为2弧度，其弦长为4sin1.

答案：2,4sin1 cm

6．sin1，cos1，tan1的大小关系是

(　)

A．tan1>sin1>cos1　 　　　　　　　　　 B．tan1>cos1>sin1

C．cos1>sin1>tan1　 　　　　　　　　　 D．sin1>cos1>tan1

解析：因为1rad≈57.30°，结合单位圆中的三角函数线知tan1>sin1>cos1，故选A.

答案：A

5．如果θ是第二象限角，且满足cos－sin＝，那么

(　)

A．是第一象限角

B．是第二象限角

C．是第三象限角

D．可能是第一象限角，也可能是第三象限角

解析：∵θ是第二象限角，∴是第一或第三象限角前半区域的角，∵cos－sin＝≥0，∴cos≥sin，∴只能在第三象限．

答案：C

4. (2010·杭州质检)如图1，已知单位圆O与y轴相交于A、B两点．角θ的顶点为原点，始边在x轴的正半轴上，终边在射线OC上．过点A作直线AC垂直于y轴且与角θ的终边交于点C，则有向线段AC的函数值是

(　)

图1

A．sinθ　 B．cosθ

C．tanθ　 D．cotθ

解析：根据单位圆中三角函数线的定义可知应选择D.　 　　　　　　　　　　　　　　

答案：D

3．若tanx>0，且sinx+cosx>0，则角x的终边在

(　)

A．第一象限　 　　　　　　　　　　　　　 B．第二象限

C．第三象限　 　　　　　　　　　　　　　 D．第四象限

解析：由tanx>0知角x在第一或第三象限，又sinx+cosx>0，故x不可能在第三象限．

答案：A

2．若α是第三象限的角，则π－α是

(　)

A．第一或第二象限的角　 　　　　 B．第一或第三象限的角

C．第二或第三象限的角　 　　　　 D．第二或第四象限的角

解析：在坐标系中，将各象限2等分，再从x轴正向的上方起，依次将各区域标上Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅰ，Ⅱ，Ⅲ，Ⅳ，则由图可知，在Ⅲ内，π－在Ⅱ内，故π－在第一或第三象限，选B.

答案：B

1．角α的终边上有一点(a，－a)(a>0)，则使f(a)＝－的一个函数是

(　)

A．f(x)＝sinx　 　　　　　　　　　　　　　 B．f(x)＝tanx

C．f(x)＝cosx　 　　　　　　　　　　　　 D．f(x)＝cotx

解析：由角的定义知sinα＝－＝－.

答案：A

13．(20分)(2009·陕西高考)已知函数f(x)＝Asin(ωx+φ)，x∈R(其中A>0，ω>0,0<φ<)的图象与x轴的交点中，相邻两个交点之间的距离为，且图象上一个最低点为M(，－2)．

(1)求f(x)的解析式；

(2)当x∈[，]时，求f(x)的值域．

解：(1)由最低点为M(，－2)得A＝2.

在x轴上相邻两个交点之间的距离为得＝，即T＝π，∴ω＝＝＝2.

由点M(，－2)在函数图象上得2sin(2×+φ)＝－2，即sin(+φ)＝－1，故+φ＝2kπ－，k∈Z，

∴φ＝2kπ－.

又φ∈(0，)，∴φ＝，故f(x)＝2sin(2x+)．

(2)∵x∈[，]，∴2x+∈[，]，

当2x+＝，即x＝时，f(x)取得最大值2；当2x+＝，即x＝时，f(x)取得最小值－1，故f(x)的值域为[－1,2]．

12．(15分)设函数f(x)＝(2cosx+asinx)sinx+cos²x(x∈R)，且f()＝f()．

(Ⅰ)求函数f(x)的值域；

(Ⅱ)设f(x)图象上过任意一点P的切线斜率为k，证明：|k|≤2.(文科选做)

解：(Ⅰ)f(x)＝2sinxcosx+asin²x+1－sin²x

＝sin2x+(1－cos2x)+1.

∴f()＝a，f()＝.

由f()＝f()，有a＝，∴a＝3.

∴f(x)＝sin2x－cos2x+2＝sin(2x－)+2.

∴函数f(x)的值域为[2－，2+]．

(Ⅱ)设P(x，y)是f(x)图象上任意一点，则

k＝f′(x)＝2cos(2x－)．

∴|k|＝|f′(x)|＝≤|2|＝2.