12．(15分)设f(x)＝x²+ax+3－a，若f(x)在闭区间[－2,2]上恒为非负数，求实数a的取值范围．

解：f(x)＝x²+ax+3－a＝²+3－a－.

f(x)≥0在x∈[－2,2]上恒成立，即f(x)在[－2,2]上的最小值非负．

(1)当－<－2，即a>4时，y_min＝f(－2)＝7－3a，由7－3a≥0，得a≤，这与a>4矛盾，此时a不存在；

(2)当－2≤－≤2，即－4≤a≤4时，y_min＝f＝3－a－，由3－a－≥0，得－6≤a≤2，此时－4≤a≤2；

(3)当－>2，即a<－4时，y_min＝f(2)＝7+a，由7+a≥0，得a≥－7，此时－7≤a<－4.

综上，所求a的范围是[－7,2]．

11．(15分)已知二次函数f(x)的二次项系数为a，且不等式f(x)>－2x的解集为(1,3)．

(1)若方程f(x)+6a＝0有两个相等的根，求f(x)的解析式；

(2)若f(x)的最大值为正数，求实数a的取值范围．

解：本题主要考查二次函数、方程的根与系数关系，考查运用数学知识解决问题的能力．

(1)∵f(x)+2x>0的解集为(1,3)．

∴f(x)+2x＝a(x－1)(x－3)，且a<0，因而

f(x)＝a(x－1)(x－3)－2x＝ax²－(2+4a)x+3a.　 ①

由方程f(x)+6a＝0，得ax²－(2+4a)x+9a＝0.②

∵方程②有两个相等的根，∴Δ＝[－(2+4a)]²－4a·9a＝0，即5a²－4a－1＝0.解得a＝1或a＝－.　　 　　　　　　　　　　　　　　

由于a<0，舍去a＝1，将a＝－代入①得

f(x)的解析式为f(x)＝－x²－x－.

(2)由f(x)＝ax²－2(1+2a)x+3a

＝a²－

及a<0，可得f(x)的最大值为－.

由

解得a<－2－或－2+<a<0.

故当f(x)的最大值为正数时，实数a的取值范围是

(－∞，－2－)∪(－2+，0)．

10．(2008·浙江高考)已知t为常数，函数y＝|x²－2x－t|在区间[0,3]上的最大值为2，则t＝________.

解析：令m＝x²－2x∈[－1,3]，y＝|m－t|的最大值在m＝－1或m＝3时取得，|－1－t|²－|3－t|²＝8(t－1)，当t≥1时，y_max＝|t+1|＝t+1＝2，∴t＝1.

当t<1时，y_max＝|3－t|＝3－t＝2，t＝1(舍去)，综合分析得t＝1.

答案：1

9．若关于x的方程3x²－5x+a＝0的一个根在(－2,0)内，另一个根在(1,3)内，则a的取值范围是________．

图1

解析：设f(x)＝3x²－5x+a(如图1所示)，则f(x)＝0的两根分别在(－2,0)、(1,3)内的充要条件是

解之，得－12<a<0.

答案：(－12,0)

8．已知A＝[1，b](b>1)，对于f(x)＝(x－1)²+1，当x∈A时，f(x)∈A，则b的值是__________．

解析：x∈[1，b]时，f(x)是增函数，故x＝b时，f(x)取最大值，即f(b)＝b，得(b－1)²+1＝b，解得b＝3或b＝1(舍去)．

答案：3

7．若f(x)＝g(x)＝x²－x(x∈R)，则方程f[g(x)]＝x的解为__________．

解析：当g(x)＝x²－x≥2，即x≤－1或x≥2时，方程f[g(x)]＝x可变为x²－x－1＝x，解得x＝1+.

当g(x)＝x²－x<2，即－1<x<2时，方程f[g(x)]＝x可变为x＝1.

所以方程f[g(x)]＝x的解为x＝1或x＝1+.

答案：x＝1或x＝1+

6．(2009·宁夏银川一模)二次函数y＝a(a+1)x²－(2a+1)x+1，当a＝1,2,3，…，n，…时，其图象在x轴上截得的弦长依次为d₁，d₂，…，d_n，…，则d₁+d₂+…+d_n为　 (　)

A.　 　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析：令a(a+1)x²－(2a+1)x+1＝0，

解得x＝或x＝，

∴函数图象与x轴的两交点的横坐标自左至右分别为和，

∴d₁+d₂+…+d_n＝1－+－+…+－＝1－＝.

答案：D

5．已知二次函数y＝ax²+bx+c满足a>b>c，且a+b+c＝0，那么它的图象是下图中的(　)

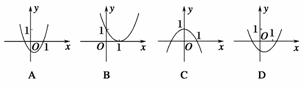
解析：首先注意到a+b+c＝0即是令解析式中x＝1得到的，即当x＝1时y＝0，也就是抛物线必过(1,0)点，因而D显然不对，又a+b+c＝0，a>b>c，可得a>0，c<0，由a>0可知C不对；由c<0可知B不对，故应选A.

答案：A

4．不等式f(x)＝ax²－x－c>0的解集为{x|－2<x<1}，则函数y＝f(－x)的图象为(　)

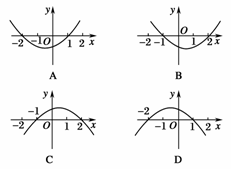
解析：由解得

∴f(x)＝－x²－x+2，∴f(－x)＝－x²+x+2，由图象知选C.

答案：C

3．已知函数f(x)＝4x²－mx+5在区间[－2，+∞)上是增函数，则f(1)的范围是(　)

A．f(1)≥25　 　　　　　　　　　　　　　　　　　 B．f(1)＝25

C．f(1)≤25　 　　　　　　　　　　　　　　　　　 D．f(1)>25

解析：y＝f(x)的对称轴是x＝，可知f(x)在[，+∞)上递增，由题设只需≤－2⇒m≤－16，

∴f(1)＝9－m≥25.

答案：A