6．函数f(x)＝log_a(x²－ax+2)在区间(1，+∞)上恒为正值，则实数a的取值范围为(　)

A．(1,2)　 　　　　　　　　　　　　B．(1,2]

C．(0,1)∪(1,2)　 　　　　　　　　　　　　　　 D．(1，)

解析：当a>1时，x²－ax+2>1，即x²－ax+1>0在x∈(1，+∞)上恒成立∴1－a+1≥0∴a≤2.∴1<a≤2；当0<a<1时，0<x²－ax+2≤1，即x²－ax+2>0且x²－ax+1≤0在x∈(1，+∞)上恒成立，无解．综上，1<a≤2，故选B.

答案：B

5．(2009·湖南高考)若log₂a<0，()^b>1，则(　)

A．a>1，b>0　 　　　　　　　　　　　　　　　　 B．a>1，b<0

C．0<a<1，b>0　 　　　　　　　　　　　　　　 D．0<a<1，b<0

解析：由log₂a<0⇒0<a<1，由^b>1⇒b<0，故选D.

答案：D

4．(2009·全国卷Ⅱ)设a＝log₃π，b＝log₂，c＝log₃，则　　　　　　　　　　　　　　 (　)

A．a>b>c　 　　　　　　　　　　　　　　　　　　　 B．a>c>b

C．b>a>c　 　　　　　　　　　　　　　　　　　　　 D．b>c>a

解析：a＝log₃π>1，b＝log₂＝log₂3∈，c＝log₃＝log₃2∈，故有a>b>c.

答案：A

3．(2009·北京高考)为了得到函数y＝lg的图象，只需把函数y＝lgx的图象上所有的点　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．向左平移3个单位长度，再向上平移1个单位长度

B．向右平移3个单位长度，再向上平移1个单位长度

C．向左平移3个单位长度，再向下平移1个单位长度

D．向右平移3个单位长度，再向下平移1个单位长度

解析：由y＝lg得y＝lg(x+3)－1，由y＝lgx图象向左平移3个单位，得y＝lg(x+3)的图象，再向下平移一个单位得y＝lg(x+3)－1的图象．故选C.

答案：C

2．(2010·深圳调研)若函数f(x)＝log_a(x+b)的图象如图1，其中a，b为常数，则函数g(x)＝a^x+b的大致图象是　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

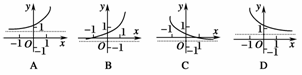
由题意得0<a<1,0<b<1，则函数g(x)＝a^x+b的大致图象是D.

答案：D

1．若函数y＝f(x)的图象与函数y＝log₂－1的图象关于直线y＝x对称，则f(x－1)＝(　)

A．4^x　　　　　　　　　　　　　　　　 B．4^x+1

C．2^x　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．2^x+1

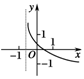
图1

解析：函数y＝log₂－1的反函数为y＝f(x)＝4^x+1，则f(x－1)＝4^x，故选A.

答案：A

13．(20分)(2009·广东中学模拟)已知△ABC的面积S满足3≤S≤3且·＝6，与的夹角为α.

(1)求α的取值范围；

(2)求f(α)＝sin²α+2sinαcosα+3cos²α的最小值．

解：(1)由题意知·＝||·||cosα＝6.

∵||·||＝，

S＝||·||sin(π－α)＝||·||sinα

＝××sinα＝3tanα.

∵3≤S≤3，∴3≤3tanα≤3即1≤tanα≤.

∵α是与的夹角，∴α∈[0，π]，∴α∈.

(2)f(α)＝sin²α+2sinαcosα+3cos²α＝1+sin2α+2cos²α＝2+sin2α+cos2α＝2+sin.

∵α∈，2α+∈，

∴当2α+＝，即当α＝时，f(α)有最小值．

f(α)的最小值是.

12．(15分)(2009·山东聊城二模)已知tan(α+)＝－.

(1)求tanα的值；

(2)求的值．

解：(1)由tan(α+)＝＝－，

得tanα＝－.

(2)原式＝

＝

＝＝＝.

11．(15分)(1)若角α是第二象限角，化简tanα；

(2)化简：.

解：(1)原式＝tanα＝tanα

＝，

∵α是第二角限角，∴sinα>0，cosα<0，

∴原式＝＝·＝－1.

(2)原式＝

＝＝＝1.

10．(2009·山东烟台二模)已知tanα+＝，则tan²α++＝__________.

解析：tanα+＝，

∴+＝＝.

∴tan²α++

＝(tanα+)²－2+

＝()²－2+＝.

答案：