10．已知点G是△ABC的重心，＝λ+μ(λ，μ∈R)，那么λ+μ＝________；若∠A＝120°，·＝－2，则||的最小值是__________．

解析：取BC的中点D，则＝＝×(+)＝+，因此λ+μ＝+＝；当∠A＝120°，·＝－2时，||·||cos120°＝－2，||·||＝4，||＝|+|＝≥＝，即||的最小值是.

答案：　

9．如图1，在△ABC中，∠BAC＝120°，AB＝2，AC＝1，D是边BC上一点，DC＝2BD，则·＝________.

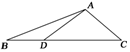
图1

解析：＝+＝+

＝+(－)＝+，

又∵＝－，||²＝1，||²＝4，

∴·＝2×1×cos120°＝－1，

∴·＝(+)·(－)

＝²－²+·＝－，故填－.

答案：－

8．(2009·广东高考)若平面向量a，b满足|a+b|＝1，a+b平行于x轴，b＝(2，－1)，则a＝________.

解析：设a＝(x，y)，则a+b＝(x+2，y－1)，

由题意⇒

∴a＝(－1,1)或(－3,1)．

答案：(－1,1)或(－3,1)

7．(2009·江苏高考)已知向量a和向量b的夹角为30°，|a|＝2，|b|＝，则向量a和向量b的数量积a·b＝________.

解析：a·b＝|a|·|b|·cosθ＝2×cos30°＝2×＝3.

答案：3

6．已知a，b是平面内两个互相垂直的单位向量，若向量c满足(a－c)·(b－c)＝0，则|c|的最大值是

(　)

A．1　 　　　　　　　　　　　　　　　　　　　 B．2

C.　 　　　　　　　　　　　　　　　　　　　 D.　 　　　　　　　　　　　　　　

解析：建立平面直角坐标系，设a＝(1,0)，b＝(0,1)，c＝(x，y)．

由(a－c)·(b－c)＝0得(x－)²+(y－)²＝.

这说明向量c的终点在圆(x－)²+(y－)²＝上，又向量c的起点O也在圆上，原点O到此圆上的点的最大值等于圆的直径的大小，即|c|_max＝.故选C.

答案：C

5．设D、E、F分别是△ABC的三边BC、CA、AB上的点，且＝2，＝2，＝2，则++与

(　)

A．反向平行　 　　　　　　　　　　　　　 B．同向平行

C．互相垂直　 　　　　　　　　　　　　　 D．既不平行也不垂直

解析：＝+＝+，

＝+＝+，

＝+＝+，

∴++＝++

＝(+)+

＝+＝－.故选A.

答案：A

4．已知非零向量和满足(AB,\s\up6(→\s\up7(　+AC,\s\up6(→\s\up7(　)·＝0，且AB,\s\up6(→\s\up7(　·AC,\s\up6(→\s\up7(　＝，则△ABC为(　)

A．三边均不相等的三角形　 　　 B．直角三角形

C．等腰非等边三角形　 　　　　　　 D．等边三角形

解析：由(AB,\s\up6(→\s\up7(　+AC,\s\up6(→\s\up7(　)·＝0⇒∠BAC的角平分线与BC垂直，∴△ABC为等腰三角形，

∵AB,\s\up6(→\s\up7(　·AC,\s\up6(→\s\up7(　＝，

∴∠BAC＝60°，∴△ABC为等边三角形．

答案：D

3．(2009·辽宁高考)平面向量a与b的夹角为60°，a＝(2,0)，|b|＝1，则|a+2b|＝(　)

A.　 　　　　　　　　　　　　　　　　　　　 B．2

C．4　 　　　　　　　　　　　　　　　　　　　 D．12

解析：∵|a|＝2，∴|a+2b|²＝(a+2b)²＝a²+4a·b+4b²＝4+4×2×1×cos60°+4×1²＝12，∴|a+2b|＝2.

答案：B

2．(2009·重庆高考)已知|a|＝1，|b|＝6，a·(b－a)＝2，则向量a与b的夹角是

(　)

A.　 　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　 D.

解析：∵a·(b－a)＝a·b－a²＝2.又|a|＝1，∴a·b＝3.即|a|·|b|cos〈a，b〉＝3＝1×6cos〈a，b〉，得cos〈a，b〉＝，∴a与b的夹角为，故选C.

答案：C　 　　　　　　　　　　　　　　

1．(2009·全国卷Ⅱ)已知向量a＝(2,1)，a·b＝10，|a+b|＝5，则|b|＝

(　)

A.　　　　　　　　　 B.

C．5　 　　　　　　　　　　　　　　　　　　　 D．25

解析：|a+b|²＝a²+2a·b+b²＝|a|²+2a·b+|b|²＝50，即5+2×10+|b|²＝50，∴|b|＝5.

答案：C