6．(2009·潍坊质检)设a＞b＞c，且+≥恒成立，则m的取值范围是________．

解析：∵a＞b＞c，∴a－b＞0，b－c＞0，a－c＞0.又(a－c)＝[(a－b)+(b－c)]×≥2 ·2＝4.当且仅当a－b＝b－c且＝　　 ，即a+c＝2b时，等号成立．∴m≤4.

答案：m≤4

5．已知a＞b＞c，则与的大小关系是________．

解析：∵a－b＞0，b－c＞0，∴≤＝，

当且仅当a－b＝b－c即2b＝a+c时，取“＝”．∴≤.

答案：≤

4．(2009·天津)设x，y∈R，a＞1，b＞1，若a^x＝b^y＝3，a+b＝2 ，则+的最大值为(　)

A．2　 　　 　B.　 　　 　C．1　 　　　　 D.

解析：由a^x＝b^y＝3得：x＝log_a3，y＝log_b3，由a＞1，b＞1知x＞0，y＞0，+＝log₃a+log₃b＝log₃ab≤log₃²＝1，当且仅当a＝b＝ 时“＝”号成立，则+的最大值为1.

答案：C

3．设a、b∈(0，+∞)，若a+b＝2，则+的最小值等于(　)

A．1　 　　　　　 B．3 　　　　　 C．2　 　　　　　 D．4

解析：因为(a+b)≥2·2，即(a+b)·≥4，其中a+b＝2，所以+≥2.当＝，且a＝b即a＝b＝1时，+取得最小值2.

答案：C

2．(2009·重庆)已知a＞0，b＞0，则++2的最小值是(　)

A．2　 　　　　　 B．2 　 　　 　C．4　 　　　　 D．5

解析：++2≥2　+2≥4　＝4

当，即a＝b＝1时，等号成立，因此++2　的最小值为4.

答案：C

1．若实数a、b满足0＜a＜b，且a+b＝1，则下列四个数中最大的是(　)

A.　 　　　　　　　 B．a²+b² 　 C．2ab　 　　　 D．a

解析：∵a+b＝1，a+b＞2，∴2ab＜.由a²+b²＞2·²＝2·＝，

又0＜a＜b，且a+b＝1，∴a＜，∴a²+b²最大．

答案：B

13．(20分)已知点M(2,3)，N(8,4)在线段MN内是否存在点P，使＝λ＝λ²(λ≠0)成立？若存在，求出对应的λ的值和P点坐标；若不存在，请说明理由．

解：由λ＝λ²即＝λ.

∴＝λ(+)，整理得＝

又＝λ，∴λ＝，即λ²+λ－1＝0.

又λ>0，∴λ＝.

∴x＝＝11－3，

y＝＝.

因此存在一点P满足条件，对应的λ＝，P点坐标为(11－3，)．

12．(15分)已知函数y＝－2(x－2)²－1经过a平移后使得抛物线顶点在y轴上，且在x轴上截得的弦长为4，求平移后的函数解析式和a.

解：设a＝(h，k)，则平移公式为

，将其代入y＝－2(x－2)²－1，

得平移后的抛物线为y′－k＝－2(x′－h－2)²－1，

即y－k＝－2(x－h－2)²－1，

∵它的顶点在y轴上，∴－h－2＝0，h＝－2，

∴y－k＝－2x²－1，

令y＝0，得2x²－k+1＝0，x＝±.

又∵|x₁－x₂|＝4，∴2＝4，

∴k＝9，∴y＝－2x²+8，a＝(－2,9)．

11．(15分)已知A(2,3)，B(－1,5)，且满足＝，＝3，＝－，求C，D，E的坐标．

解：解法1：设C(x_C，y_C)，D(x_D，y_D)，E(x_E，y_E)．

∴＝(x_C－2，y_C－3)，＝(－3,2)．

＝(x_D－2，y_D－3)，＝(x_E－2，y_E－3)．

由条件得(x_C－2，y_C－3)＝(－3,2)，

(x_D－2，y_D－3)＝3(－3,2)，

(x_E－2，y_E－3)＝－(－3,2)．从而有

，，.

∴C(1，)，D(－7,9)，E(，)．

解法2：由＝3＝3(+)得＝－.

由＝－(+)，得＝－.

由＝＝(+)，得＝.

由定比分点公式，可得

x_C＝＝1，y_C＝＝；

x_D＝＝－7，

y_D＝＝9；

x_E＝＝，

y_E＝＝.

∴C(1，)，D(－7,9)，E(，)．

10．(2009·福建质检)P为△ABC所在平面上的点，且满足＝+，则△ABP与△ABC的面积之比是________．

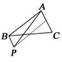
图3

解析：∵＝+，∴＝

∴P点位置如图3所示：∴＝

答案：1?2