
3.例题
(1)火车以速度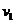 匀速行驶,司机发现前方同轨道上相距S处有另一列火车沿同方向以速度
匀速行驶,司机发现前方同轨道上相距S处有另一列火车沿同方向以速度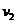 (对地、且
(对地、且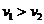 )做匀速运动,司机立即以加速度
)做匀速运动,司机立即以加速度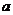 紧急刹车,要使两车不相撞,
紧急刹车,要使两车不相撞,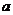 应满足什么条件?
应满足什么条件?
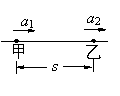 (2)如图所示,处于平直轨道上的甲、乙两物体相距为s,同时、同向开始,甲以初速度v、加速度a1做匀加速直线运动,乙做初速度为零、加速度a2的匀加速直线运动,假设甲能从乙旁边通过,下述情况可能发生的是( )
(2)如图所示,处于平直轨道上的甲、乙两物体相距为s,同时、同向开始,甲以初速度v、加速度a1做匀加速直线运动,乙做初速度为零、加速度a2的匀加速直线运动,假设甲能从乙旁边通过,下述情况可能发生的是( )
A.a1=a2时,能相遇两次
B.a1>a2时,能相遇两次
C.a1<a2时,能相遇两次
D.a1<a2时,能相遇一次
(3)甲、乙两运动员在训练交接棒的过程中发现:甲经短距离加速后能保持9m/s的速度跑完全程;乙从起跑后到接棒前的运动是匀加速的。为了确定乙起跑的时机,需在接力区前适当的位置设置标记。在某次练习中,甲在接力区前S0=13.5m处作了标记,并以V=9m/s的速度跑到此标记时向乙发出起跑口令。乙在接力区的前端听到口令时起跑,并恰好在速度达到与甲相同时被甲追上,完成交接棒。已知接力区的长度为L=20m。
求:(1)此次练习中乙在接棒前的加速度a;
(2)在完成交接棒时乙离接力区末端的距离。
解答:(1)在甲发出口令后,甲乙达到共同速度所用时间为:  ,在这段时间内甲、乙的位移分别为S1和S2,则
,在这段时间内甲、乙的位移分别为S1和S2,则 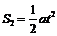
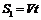 ,
,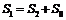 联立解得:
联立解得: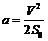 ,
,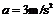 。
。
(2)在这段时间内,乙在接力区的位移为: ,
,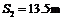 。完成交接棒时,乙与接力区末端的距离为
。完成交接棒时,乙与接力区末端的距离为
3、相遇
(1)同向运动的两物体的相遇问题即追及问题,分析同上。
(2)相向运动的物体,当各自发生的位移绝对值的和等于开始时两物体间的距离时即相遇。
2、追及问题的特征及处理方法:
“追及”主要条件是:两个物体在追赶过程中处在同一位置,常见的情形有三种:
⑴ 初速度为零的匀加速运动的物体甲追赶同方向的匀速运动的物体乙,一定能追上,追上前有最大距离的条件:两物体速度 ,即 。
⑵ 匀速运动的物体甲追赶同向匀加速运动的物体乙,存在一个能否追上的问题。
判断方法是:假定速度相等,从位置关系判断。
①若甲乙速度相等时,甲的位置在乙的后方,则 ,此时两者之间的距离 。
②若甲乙速度相等时,甲的位置在乙的前方,则 。
③若甲乙速度相等时,甲乙处于同一位置,则 ,为临界状态。
解决问题时要注意二者是否同时出发,是否从同一地点出发。
⑶ 匀减速运动的物体追赶同向的匀速运动的物体时,情形跟⑵类似。
1、追及问题中两者速度大小与两者距离变化的关系。
甲物体追赶前方的乙物体,若甲的速度大于乙的速度,则两者之间的距离 。若甲的速度小于乙的速度,则两者之间的距离 。若一段时间内两者速度相等,则两者之间的距离 。
3.练习题:
有一列火车,每节车厢的长度为L,车厢间的间隙宽度不计,挨着车头的第一节车厢前沿站台上站着一人,当火车从静止开始以加速度a作匀变速直线运动时,第n节车厢经过人的时间为___________________。
2.例题:
(1)物体从静止开始沿斜面匀加速下滑,它通过斜面的下一半的时间是通过上一半时间的n倍,则n为: ( )
A. 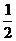 B.
B. 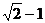 C. 1 D. 2
C. 1 D. 2
(2)五辆汽车每隔一定时间,以同一加速度从车站沿一笔直公路出发,当最后一辆汽车起动时,第一辆汽车已离站320米,此时刻第一辆与第二辆车的距离是 米
1.内容:初速度为零的匀变速直线运动(设t为等分时间间隔)
⑴1t末、2t末、3t末、…、nt末瞬时速度之比为
v1∶v2∶v3∶…∶vn=
⑵1t内、2t内、3t内、…、nt内位移之比为
s1∶s2∶s3∶…∶sn=
⑶在连续相等的时间间隔内的位移之比为
sⅠ∶sⅡ∶sⅢ∶…∶sn=
⑷通过1s、2s、3s、…、ns的位移所用的时间之比为
t1∶t2∶t3∶…∶tn=
⑸经过连续相同位移所用时间之比为
tⅠ∶tⅡ∶tⅢ∶…∶tn=
典型应用:自由落体运动
3.练习题
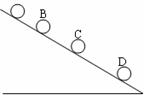 从斜面上某位置,每隔0.1 s释放一个小球,在连续释放几个后,对在斜面上的小球拍下照片,如图所示,测得sAB =15 cm,sBC =20 cm,试求
从斜面上某位置,每隔0.1 s释放一个小球,在连续释放几个后,对在斜面上的小球拍下照片,如图所示,测得sAB =15 cm,sBC =20 cm,试求
(1)小球的加速度.
(2)拍摄时B球的速度vB=?
(3)拍摄时sCD=?
(4)A球上面滚动的小球还有几个?
2.例题
(1)一列火车作匀变速直线运动驶来,一人在轨道旁观察火车的运动,发现在相邻的两个10s内,火车从他面前分别驶过8节车厢和6节车厢,每节车厢长8m(连接处长度不计)。求:
⑴火车的加速度a;
⑵人开始观察时火车速度的大小。
(2)自来水由水管口滴出水滴,每两个相邻水滴滴出的时间间隔基本上是相等的,在水管口的正下方,倒扣一个小盆,水滴滴到盆底,发出响声.逐渐向上移动小盆,直到看到水滴从水管口刚好滴出时,恰听到水滴落到盆底的响声,记录盆底距地面的高度H1=10cm,再继续上移小盆,第二次、第三次看到水从水管口滴出同时听到水滴到盆底的响声,分别测出H2=75cm,H3=130cm,g取10m/s2.求:
(1)相邻水滴滴出的时间间隔;
(2)自来水水管口离地面的高度.(0.1s,255cm)
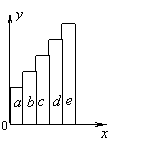 (3)在“利用打点计时器测定匀加速直线运动加速度”的实验中,某同学在打出的纸带上每5点取一个计数点,共取了A、B、C、D、E、F六个计数点(每相邻两个计数点间的四个点未画出)。从每一个计数点处将纸带剪开分成五段(分别叫a、b、c、d、e段),将这五段纸带由短到长紧靠但不重叠地粘在xoy坐标系中,如图所示,由此可以得到一条表示v-t关系的图线,从而可求出加速度。
(3)在“利用打点计时器测定匀加速直线运动加速度”的实验中,某同学在打出的纸带上每5点取一个计数点,共取了A、B、C、D、E、F六个计数点(每相邻两个计数点间的四个点未画出)。从每一个计数点处将纸带剪开分成五段(分别叫a、b、c、d、e段),将这五段纸带由短到长紧靠但不重叠地粘在xoy坐标系中,如图所示,由此可以得到一条表示v-t关系的图线,从而可求出加速度。

⑴请你在xoy坐标系中用最简洁的方法作出能表示v-t关系的图线(作答在题卡上),并指出哪个轴相当于v轴?答: 。
⑵从第一个计数点开始计时,要想求出0.15s时刻的瞬时速度,需要测出哪一段纸带的长度?答: 。
(3)若测得a段纸带的长度为2.0cm,e段纸带的长度为10.0cm,则加速度为 m/s2。
1.内容:
⑴匀变速直线运动的物体在连续相邻相等时间内的位移之差相等,等于加速度和时间间隔平方和的乘积。即 , 可以推广到
, 可以推广到
Sm-Sn= 。
试证明此结论:
典型应用:打点计时器纸带加速度的计算。
⑵物体在某段时间(初速为v0末速为vt)的中间时刻的瞬时速度等于该段时间内的平均速度。vt/2= 。
典型应用:打点计时器纸带瞬时速度的计算。
⑶某段位移(初速为v0末速为vt)的中间位置的瞬时速度公式,vs/2= 。可以证明,无论匀加速直线运动还是匀减速直线运动均有有vt/2 vs/2。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com