
重点:整合知识、构建单元知识系统.
难点:提升综合应用能力.
3.情感、态度与价值观
在学习过程中,通过知识整合,能力培养,激发学生的学习兴趣. 养成合作、交流的良好学习品质.
2.过程与方法
在整合函数性质、综合运用函数性质的过程中,培养学生分析、观察、思考的教学能力、提升学生的归纳、推理能力.
1.知识与技能
整合函数性质建构知识网络,以便于进一步理解和掌握函数的性质.提升综合运用函数性质的能力. 
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
回顾反思 构建体系 |
  |
师:要求学生借助课本回顾第一章的第1、2节的基本知识.  生:独立回顾总结第1、2节的基本知识.  师生合作:学生口述单元知识,老师用网络图的形式板书知识构造体系图. |
整合知识,形成单元知识系统. 培养归纳概括能力. |
示例剖析 升华能力(I) |
   例1 设A、B、I均为非空集合,且满足A?B?I,则下列各式中错误的是( )  A.( 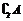 )∪B = I )∪B = I B.( 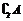 )∪( )∪(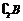 ) =I ) =I C.A∩( 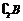 ) = ) =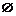  D.( 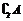 )∩( )∩(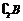 ) = ) =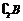    例2 已知集合A = {x| –2<x<–1或x>0},B = {x| a≤x≤b},满足A∩B = {x | 0<x≤2},A∪B = {x| x>– 2}.  求a、b的值.  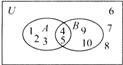  例3 集合P = {x | x2 + x – 6 = 0},  Q = {x | mx– 1 = 0},且Q 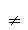  P,求实数m的取值集合. P,求实数m的取值集合.  |
生:尝试完成例1~例3. 并由学生代表板书例1 ~ 例3的解题过程.  师生合作点评学生代表的解答,并分析解题思路的切入点和寻找解题的最优途径.  例1解析:本题主要考查子集及运算.  答案:B  如图    例2解析:将集合A、A∩B、A∪B分别在数轴上表示,如图所示,由A∩B = {x | 0<x≤2}知b =2且–1≤a≤0;  由A∪B = {x | x>– 2},知–2<a≤–1,  综上所知,a = –1,b =2.  例3解析:P = {2,– 3},Q 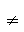  P,∴Q = P,∴Q =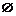 ,Q = {2}或Q = {– 3}. ,Q = {2}或Q = {– 3}. ①当Q = Q 时,m = 0;  ②当Q = {2}时,2m – 1= 0,即m = 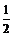 ; ; ③当Q = {– 3}时,–3m –1 = 0,即m = 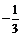 . .综上知,m的取值的集合为{0, 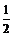 , ,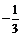 }. }. |
通过尝试练习,训练思维.通过合作交流探索题途径 |
|
经典例题 |
例4 求下列函数的定义域: (1)y = 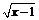 + +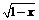 ; ;(2)y = 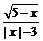 . .例5 求下列函数的值域: (1)y = x2 –2x,x?[0,3]; (2)y = x + 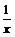 ,x?[0,+∞]; ,x?[0,+∞];(3)y = x + 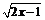 ; ;(4)y = |x+1| + |x– 2|. 例6 已知函数f (x)的解析式为: 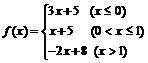 . .(1)求f ( 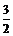 ),f ( ),f (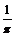 ),f (–1)的值; ),f (–1)的值;(2)画出这个函数的图象; (3)求f (x)的最大值. |
例4解析:(1)由,得x = 1, ∴函数的定义域为{1}. (2)由题意知,有不等式组 , 即x<–3或–3<x<3或3<x≤5. 故函数y =的定义域为 (–∞,–3)∪(–3,3)∪(3,5]. 例5解析:(1)y = x2 –2x = (x – 1)2 –1,如图所示,y ?[–1,3]为所求. (2)配方得y = x +, 当且仅当 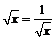 ,即x = 1时,y =2, ,即x = 1时,y =2,∴y?[2,+∞]为所求. (3)换元法 令 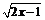 = t,t≥0,则x = = t,t≥0,则x =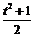 , ,函数化为y = 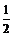 t2
+ t2
+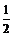 = 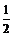 (t
+1) 2, (t
+1) 2,∵t≥0,∴y≥ 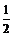 , ,∴函数y = x + 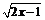 的值域为[ 的值域为[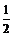 ,+∞]. ,+∞].(4)方法一:运用绝对值的几何意义. |x +1| + |x– 2|的几何意义表示数轴上的动点x与–1以及2的距离的和,结合数轴,易得|x + 1| + |x– 2|≥3, ∴函数的值域为y?[3,+∞). 方法二:转化为函数图象,运用数形结合法. 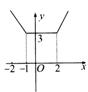 函数y = |x +1| + |x– 2|的零点为–1,2,把定义域分成三区间 (– ∞,–1],(–1,2],[2,+∞). ∴ 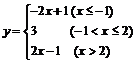 . .该函数图象如图所示,由图象知函数的值域为[3,+∞]. 例6解析:(1)∵ 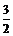 >1, >1,∴f ( 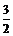 ) = –2×( ) = –2×(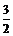 ) + 8 =5, ) + 8 =5,∵f ( 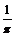 ) = ) =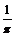 +5 = +5 =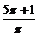 . .∵–1<0,∴f (–1) = –3+5 =2. 如图 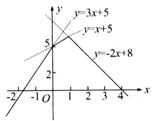 在函数y =3x +5图象上截取x≤0的部分, 在函数y = x +5图象上截取0<x≤1的部分, 在函数y = –2x +8图象上截取x>1的部分. 图中实线组成的图形就是函数f (x)的图象. (3)由函数图象可知 当x = 1时,f (x)的最大值为6. |
通过尝试练习,训练思维.通过合作交流探索题途径. 归纳总结求函数定义域的题型及方法. 归纳总结求函数值域的题型及方法. |
|
布置作业 |
见单元小结1的习案 |
学生独立完成 |
巩固旧知提升能力 |
备选例题
例1 对于集合A = {x|x2 – 2a x
+ 4a – 3 = 0},B ={x| x2 –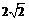 ax
+ a 2 + a + 2 = 0},是否存在实数a,使A∪B =
ax
+ a 2 + a + 2 = 0},是否存在实数a,使A∪B =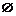 ?若a不存在,说明理由,若a存在,求出a的值.
?若a不存在,说明理由,若a存在,求出a的值.
分析:A∪B =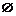 ,即A =
,即A =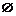 且B =
且B =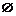 ,只要两个方程能同时无解即可.
,只要两个方程能同时无解即可.
∵A∪B =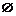 ,∴A =
,∴A =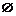 且B =
且B =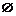 .
.
由△1<0且△2<0得
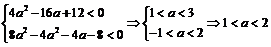 .
.
所以存在这样的实数a?(1,2)使得A∪B =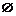 .
.
例2(1)已知函数f (2x–1)的定义域为[0,2],求f (x)的定义域;
(2)已知函数f (x)的定义域为[–1,3],求f (2x–1)定义域.
[解析](1)由f (2x–1)的定义域为[0,2],
即x∈[0,2],∴2x–1∈[–1,3].
令t =2x–1,则f (t)与f (x)为同一函数,
∴t的范围[–1,3]即f (t)的定义域,∴f (x)的定义域为[–1,3].
(2)求f (2x–1)的定义域,
即由2x–1∈[–1,3]求x的范围,
解得x∈[0,2].
自主探究与合作交流相结合. 自主探究知识的纵模联系,合作交流归纳整理知识,构建单元知识体系.
重点:构建知识体系;难点:整合基本数学知识、数学思想和数学方法.
3.情感、态度与价值观
在知识的回顾、整理过程中体会数学知识的整体性和关联性. 感受数学的系统化与结构化的特征.
2.过程与方法
通过知识的整理,知识与方法的综合应用,加深对知识的理解.提升应用基本方法的能力.,从而使学生系统地掌握的知识与方法.
1.知识与技能
(1)通过回顾集合与函数的概念及表示法,构建单元知识网络;整合知识,使知识系统化.
(2)进一步提升学生的集合思想与函数思想.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com