
2.同位素示踪法是利用 。
1.反应机理又称 ,指 。
3. 手性碳原子是指: 的碳原子。
手性分子是指: 的有机物。
手性分子具有
现象
2.现代化学测定有机化合物结构
|
分析方法 |
氢核磁共振 |
红外光谱 |
质谱 |
|
分析 原理 |
根据谱图中不同的峰,确定
,根据峰的面积确定
。 |
根据谱图可得出有机物含有
。 |
通过对样品的离子的质荷比的分析而实现对样品进行定性和定量的一种方法。主要用以确定
。 |
1.人们在研究有机化合物时首先研究其所具有的基团,如 等。(写出常见的基团)
2.元素组成的确定: 李比希法,实际为 ,根据生产物判断原有机物中所含 。
1.最简式:又称为 ,指有机化合物中所含各元素原子个数的 。
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
回顾反思 构建体系 |
函数性质单元知识网络 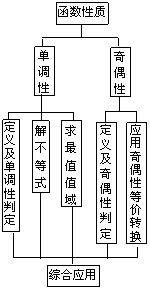  |
生:借助课本.并回顾学习过程. 整理函数掌握函数的有关性质归纳知识的纵横联系. 师生合作:学生口述单元基本知识及相互联系,老师点评、阐述、板书网络图. |
整理知识,培养归纳能力.  形成知识网络系统. |
经典例题 剖 析  升华能力 |
  例1试讨论函数f (x) = 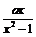 ,x(–1,1)的单调性(其中a≠0). ,x(–1,1)的单调性(其中a≠0).          例2 试计论并证明函数y = f (x) = x + 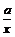 (a>0)在定义域上的单调性,函数在(0,+∞)上是否有最小值? (a>0)在定义域上的单调性,函数在(0,+∞)上是否有最小值?                       例3 已知f (x)是定义在(0,+∞)上的增函数,且满足f (xy) =  f (x) + f (y),f (2) =1.  (1)求证:f (8) =3;  (2)解不等式  f (x) – f (x–2) >3.      例4 已知函数f (x),当x、y∈R时,恒有f (x + y) = f (x) + f ( y).  (1)求证:f (x)是奇函数;  (2)如果x∈R+ ,f (x)<0,并且f (1) = 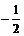 ,试求f (x)在区间[–2,6]上的最值. ,试求f (x)在区间[–2,6]上的最值. |
师生合作:学生独立尝试完成例1 ~ 例4并由学生代表板书解答过程. 老师点评. 师生共同小结解题思络. 例1[解析]设–x<x1<x2<1, 即△x = x2–x1>0, 则△y = f (x2) – f (x2) = = ∵–1<x1<x2<1, ∴x1–x2<0,–1<0,–1<0. |x1x2|<1,即 –1<x1x2<1,x1x2 +1>0, ∴<0. 因此,当a>0时,△y = f (x2) – f (x1)<0, 即f (x1)>f (x2),此时函数为减函数; 当a<0时,△y = f (x2) – f (x1) >0, 即f (x1)<f (x2),此时函数为增函数. 例2[解析]函数y = x +(a>0)在区间(–∞,–)上是增函数,在区间[–,0]上是减函数,在区间 (0,]上是减函数,在区间(,+∞)上是增函数. 先证明y = x +(a>0)在(0,+∞)上的增减性, 任取0<x1<x2, 则△x = x1–x2<0, △y = f (x1) – f (x2) = (x1 +) – (x2 +) = (x1–x2) + (–) = (x1–x2) + = (x1–x2) (1–) =△x. ∵0<x1<x2, ∴△x = x1–x2<0,x1x2>0. (1)当x1,x2∈(0,)时,0<x1x2<a,∴x1x2 – a<0, 此时①>0时, △y = f (x1) – f (x2)>0, ∴f (x)在(0, 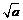 )上是减函数. )上是减函数.(2)当x1,x2∈[ 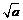 ,+∞)时,x1x2>a,∴x1x2 –
a>0, ,+∞)时,x1x2>a,∴x1x2 –
a>0,此时①<0,△y= f (x1) – f (x2)<0, ∴f (x)在[ 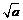 ,+∞)上是增函数, ,+∞)上是增函数,同理可证函数f (x)在(–∞,– 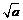 )上为增函数, )上为增函数,在[– 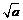 ,0)上为减函数. ,0)上为减函数.由函数f (x) = x + 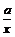 在[0, 在[0,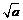 )上为减函数,且在[ )上为减函数,且在[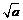 ,+∞)上为增函数知道,f (x)≥f ( ,+∞)上为增函数知道,f (x)≥f (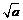 ) =2 ) =2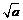 ,其中x∈(0,+ ∞), ,其中x∈(0,+ ∞),∴f (x)min=2 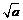 , ,也可以配方求f (x) = x + 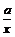 (a>0)在(0,+∞)上的最小值, (a>0)在(0,+∞)上的最小值,∴f (x) = x + 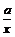 = ( = (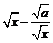 )2 + 2 )2 + 2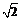 , ,当且仅当x = 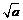 时,f (x)min =2 时,f (x)min =2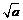 . .例3[解析](1)在f (xy) = f (x) + f (y)中, 设x = y =2,则有f (4)=f (2)+f (2), 设x= 4,y =2, 则有f (8) = f (4) + f (2) =3 f (2) = 3. (2)由f (x) – f (x–2)>3, 得f (x)>f (8) + f (x–2) = f [8 (x–2)], ∵f (x) 是(0,+∞)上的增函数, ∴ 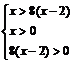 ,解得2<x< ,解得2<x<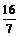 , ,故原不等式的解集为{x|2<x< 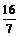 }. }.例4[解析](1)∵函数定义域为R,其定义域关于原点对称, ∵f (x + y) = f (x) + f ( y), 令y = –x,x、– x∈R, 代入f (x + y) = f (x) + f ( y), ∴f (0) = f (0) + f (0),得f (0) = 0, ∴f (x) + f (–x) = 0,得 f (–x) = – f (x), ∴f (x)为奇函数. (2)设x、y∈R+, ∵f (x+y) = f (x) + f ( y), ∴f (x+y) – f (x) = f ( y), ∵x∈R+,f (x)<0, ∴f (x+y) – f (x)<0, ∴f (x+y)<f (x). ∵x+y<x, ∴f (x)在(0,+∞)上是减函数. 又∵f (x)为奇函数, f (0) = 0, ∴f (x)在(–∞,+∞)上是减函数. ∴在区间[–2,6]上f (–2)为最大值,f (6)为最小值. ∵f (1) = 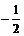 , ,∴f (–2)= – f (2) = –2 f (1) =1, f (6) = 2 f (3)=2[ f (1) + f (2)] = –3, ∴f (x)在区间[–2,6]上的最大值为1,最小值为–3. |
动手尝试练习,培养并提高解题能力. |
备选例题
例1 用定义证明函数y = f (x) =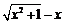 是减函数.
是减函数.
[解析]∵x2 +1>0对任意实数x均成立,
∴函数y = f
(x) =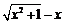 的定义域是R,
的定义域是R,
任取x1、x2∈R,且x1<x2,则△x = x2–x1>0,
△y = f (x2) – f (x1)
=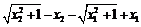
=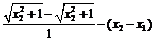
=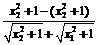 – (x2–x1)
– (x2–x1)
=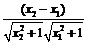 (x2
+ x1–
(x2
+ x1–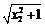 –
–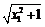 ),
),
∵x1∈R,x2∈R,且x1<x2,
∴x2–x1>0,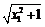 >
>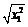 = |x1|≥x1,
= |x1|≥x1,
∴x1–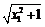 <0,同理x2–
<0,同理x2–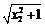 <0,
<0,
x1 + x2–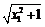 –
–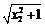 <0,
<0,
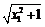 +
+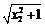 >| x1| + | x2 |>0,
>| x1| + | x2 |>0,
∴f (x2) – f (x1) <0,
∴y = f
(x) =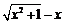 在R上是减函数.
在R上是减函数.
例2 已知函数f (x)的定义域为R,满足f (–x) =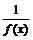 >0,且g (x) = f (x) + c(c为常数)在区间[a,b]上是减函数. 判断并证明g (x)在区间[– b,– a]上的单调性.
>0,且g (x) = f (x) + c(c为常数)在区间[a,b]上是减函数. 判断并证明g (x)在区间[– b,– a]上的单调性.
解析:设– b≤x1<x2≤– a,
则△x = x2 – x1>0,b≥–x1>–x2≥a,
∵g (x)在区间[a,b]上是减函数,
∴g (–x1)<g (–x2),即f (–x1) + c<f (–x2) + c,
则f (–x1)<f (–x2),又∵f (–x) =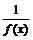 >0,
>0,
∴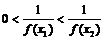 ,即f (x1)>f (x2)
,即f (x1)>f (x2)
∴f (x1) + c>f (x2) + c,即g (x1)>g(x2),
△y = g (x2) – g (x1)<0,
∴g (x)在区间[– b,– a]上是减函数.
动手练习与合作交流相结合. 在回顾、反思中整合知识,在综合问题探究、解答中提升能力. 加深对知识的准确、到位的理解与应用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com