180. 如图：ABCD-A₁B₁C₁D₁是正方体.求证：(1)A₁C⊥D₁B₁；(2)A₁C⊥BC₁

解析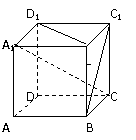：(1)连A₁C₁，则A₁C₁⊥B₁D₁，

又CC₁⊥面A₁C₁，由三垂线定理可知A₁C⊥B₁D₁，(2)连B₁C，

仿(1)可证；

179. 如图：在斜边为AB的R_t△ABC中，过点A作PA⊥平面ABC，AE⊥PB于E，AF⊥PC于F，(1)求证：BC⊥平面PAC；(2)求证：PB⊥平面AEF.

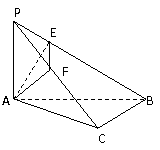
解析：

(1)PA⊥面ACB，∴PA⊥BC，BC⊥AC，∴BC⊥面PAC．(2)(1)知BC⊥AF，

又AF⊥PC，∴AF⊥面PBC，∴AF⊥PB，又PB⊥AE，∴PB⊥面AEF.

177. 如图：在△ABC中，∠ACB＝90⁰，M是AB的中点，PM⊥平面ABC，

求证：PA＝PB＝PC.

解析：连结MC，由∠ACB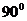＝，M为AB的中点，MB＝MC＝MA，

∴PM⊥面ABC，∴∠PMA＝∠PMB＝∠PMC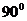＝，又PM公用，∴△PMA≌△PMB≌△PMC，∴PA＝PB＝PC；178. 四边形ABCD是距形，AB＝2，BC＝1，PC⊥平面AC，PC＝2，求点P到BD的距离.

解析：作CE⊥BD于E，连结PE，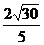

176.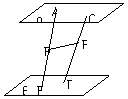 已知(如图)：平面α∥平面β, A、C∈α,B、D∈β,AB与CD是异面直线,E、F分别是线段AB、CD的中点,求证：EF∥β.

解析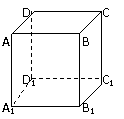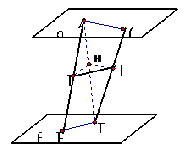：如图作辅助线，可得中线平行。

175. 棱长为1的的正方体ABCD-A₁B₁C₁D₁中,求证：平面A₁BD∥平面CB₁D₁.

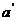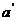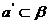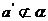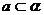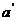
解析：过a和直线b上任意一点P作一平面γ和平面β交于，∵α∥β，∴a∥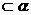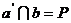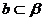，∵，，，∴，∵，，b∥β，

∴α∥β；8．∵A₁B∥D₁C，∴A₁B∥平面CD₁B₁，同理BD∥平面CD₁B₁，

∵A₁B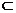面A₁BD，BD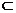面A₁BD，∴面A₁BD∥面CD₁B_1­­.

173. 如果把两条异面直线称作“一对”，则在正方体十二条棱中，共有异面直线(　 )对

A．12　　　　 B．24　　　　 C．36　　　　　 D．48

解析：B

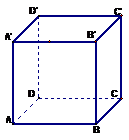如图，棱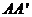有4条与之异面，所有所有棱能组成4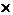12=48对，但每一对都重复计算一次，所以有48对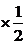=24对。174. 已知正方形ABCD所在的平面和正方形ABEF所在的平面相交于AB，M、N分别是对角线AC、BF上的点,且AM=FN,求证：MN∥平面BCE.

解析：作NP∥AB交BE于点P，作MQ∥AB交BC于点Q，

证MNPQ是平行四边形，再证MN∥面BCE.

172.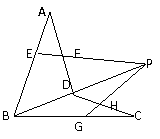 如图：已知E、F、G、H分别是空间四边形ABCD各边AB、AD、CB、CD上的点，且直线EF和HG交于点P，求证：点B、D、P在同一条直线上。

解析：∵直线EF∩直线,HG＝P，∴P∈直线EF，又EF平面ABD，

∴P∈平面ABD，同理P∈平面CBD，由公理2，点B、D、P

在同一条直线上。

171. 如图：已知△ABC在平面α外，AB∩α＝P，AC∩α＝R，BC∩α＝Q。

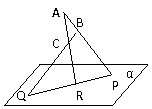求证:P、Q、R三点共线。

解析：点在线上，线在面内，可得点在面内，证明P，Q，R三个点是平面

与平面ABC的公共点，即可。

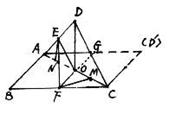
160. 把正方形ABCD沿对角线AC折成直二面角B-AC-D，E、F分别为AD、BC的中点，O为正方形的中心，求折起后∠EOF的大小

证明：过F作FM⊥AC于M，过E作EN⊥AC于N，则M，N分别为OC、AO的中点

解析：

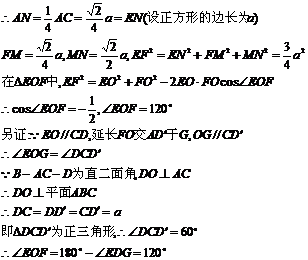
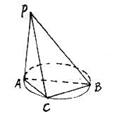
158. 设△ABC内接于⊙O，其中AB为⊙O的直径，PA⊥平面ABC。

　 如图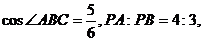求直线PB和平面PAC所成角的大小

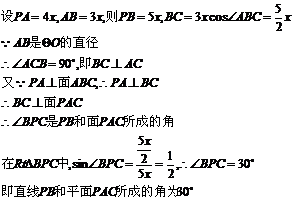
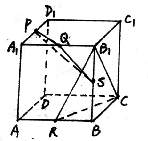　 159. 如图，在正方体ABCD-A₁B₁C₁D₁中，已知P，Q，R，S分别为棱A₁D₁，A₁B₁，AB，BB₁的中点，求证：平面PQS⊥平面B₁RC.(12分)

证明：连结BC₁交B₁C于O，则O为BC₁的中点

连结RO，AC₁，∵R是AB的中点　 ∴RO∥AC₁

∵P,Q分别为A₁D₁，A₁B₁的中点，易知A₁C₁⊥PQ

∴AC₁⊥PQ(三垂线定理)