
198.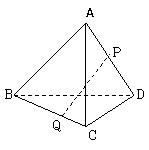 空间四边形ABCD的各边与两条对角线的长都为1,点P在AD上移动,点Q在CB上移动,求点P与点Q的最短距离。
空间四边形ABCD的各边与两条对角线的长都为1,点P在AD上移动,点Q在CB上移动,求点P与点Q的最短距离。
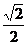
解析: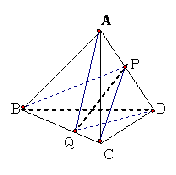 如图作辅助线,可得PQ为AD,BC的公垂线。在直角三角形BQP中可求得。
如图作辅助线,可得PQ为AD,BC的公垂线。在直角三角形BQP中可求得。
197. 已知直线l与平面α内交于一点O的三条直线OA、OB、OC成等角,求证:l⊥α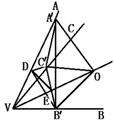
解析:若l过O点,在l上任取一点P,作PH⊥α,垂足H,则H即在∠AOB的平分线上,又在∠BOC的平分线上,∴H是它们的公共点,故H与O重合;若l不过O点,可作过O的直线l′,使l′∥l即可证明.
196. 在直角BVC的角顶点V,作直角所在平面的斜线VA,使二面角A-VB-C与二面角A-VC-B都等于45°,求二面角B-VA-C的度数.
解析:在VA上取A′作平面VCB的垂线,垂足为O,作OC′⊥VC,OB′⊥VB,连A′C′、A′B′,则∠A′C′O和∠A′B′O分别为二面角A-VC-B与二面角A-VB-C的平面角.易证VB′OC′为正方形.设VB′=a,可求得A′B′=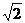 a.VA′=
a.VA′=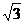 a.过B′作B′D⊥VA,
a.过B′作B′D⊥VA,
连结C′D.则∠B′DC′为二面角B-VA-C的平面角.在RtΔB′VA′中,可求B′D=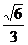 a,又DE⊥B′C′,B′E=
a,又DE⊥B′C′,B′E=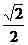 a,则在RtΔB′DE中可求得∠B′DE=60°.二面角B-VA-C为120°.
a,则在RtΔB′DE中可求得∠B′DE=60°.二面角B-VA-C为120°.
195. .如图,ABCDEF为正六边形,将此正六边形沿对角线AD折叠.

(1)求证:AD⊥EC,且与二面角F-AD-C的大小无关;
(2)FC与FE所成的角为30°时,求二面角F-AD-C的余弦值.
解析:(1)正六边形ABCDEF,在折叠前有AD⊥EC,设AD与EC交于M,折叠后即有AD⊥ME,AD⊥MC.则AD⊥平面EMC,无论∠EMC的大小如何,总有AD⊥EC.(2)利用余弦定理,有cos∠EMC=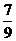
194. 已知二面角A-BC-D为150°,ΔABC是边长为a的等边三角形,ΔBCD是斜边为BC的等腰直角三角形.求两个顶点A和D间的距离.
解析:.取BC的中点E,连DE和AE,利用余弦定理AD=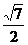 a
a
193. 正三棱柱ABC-A1B1C1中,各棱长均为2,M为AA1中点,N为BC的中点,则在棱柱的表面上从点M到点N的最短距离是多少?并求之.
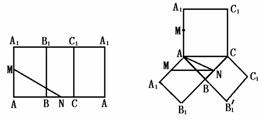
解析: (1)从侧面到N,如图1,沿棱柱的侧棱AA1剪开,并展开,则MN=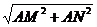 =
=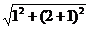 =
=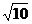
(2)从底面到N点,沿棱柱的AC、BC剪开、展开,如图2.
则MN=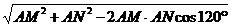
=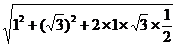 =
=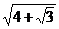
∵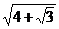 <
<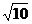
∴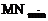 =
=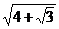 .
.
192. 如图所示,已知三棱锥S-ABC中,SA=SB=SC,且AC2+BC2=AB2,由此可推出怎样的结论?
解析: 引SO⊥平面ABC(O为垂足),连结OC.
∵SA=SB=SC,∴OA=OB=OC,
∴O是ΔABC的外心,(结论1)
又∵AC2+BC2=AB2,
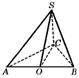
∴ΔABC是直角三角形,且AB是斜边,故O是斜边AB的中点.因而
SO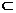 平面SAB(结论2)
平面SAB(结论2)
∴平面SAB⊥平面ABC(结论3)
191. 如图1所示,边长AC=3,BC=4,AB=5的三角形简易遮阳棚,其A、B是地面上南北方向两个定点,正西方向射出的太阳光线与地面成30°角,试问:遮阳棚ABC与地面成多大角度时,才能保证所遮影面ABD面积最大?
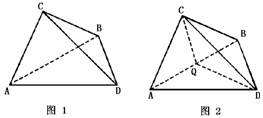
解析: 易知,ΔABC为直角三角形,由C点引AB的垂线,垂足为Q,则应有DQ为CQ在地面上的斜射影,且AB垂直于平面CQD,如图2所示.
因太阳光与地面成30°角,所以∠CDQ=30°,又知在ΔCQD中,CQ=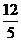 ,由正弦定理,有
,由正弦定理,有
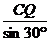 =
=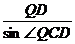 ,
,
即
QD=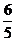 sin∠QCD.
sin∠QCD.
为使面ABD的面积最大,需QD最大,这只有当∠QCD=90°时才可达到,从而∠CQD= 60°.
故当遮阳棚ABC与地面成60°角时,才能保证所遮影面ABD面积最大.
190. P是△ABC所在平面外一点,PA、PB、PC两两垂直,G为△PAB的重心,E、F分别是BC、PB 上的点,且BE∶EC=PF∶FB=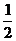 ,求证:平面GEF⊥平面PBC
,求证:平面GEF⊥平面PBC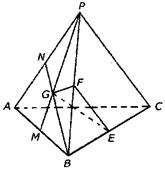
解析:∵G为△PAB的重心,∴ ∴GF∥PA.
∴GF∥PA.
∵PA⊥PB PA⊥PC,∴PA⊥面PBC.∴GF⊥面PBC,∴面GFE⊥面PBC.
189. 在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC,且分别交AC和SC于D和E,又 SA=AB,SB=BC.求以BD为棱,以BDE与BDC为面的二面角度数.
∵E为SC的中点 ∴BE⊥SC ∴SC⊥面BDE SC⊥BD 面SA⊥BD ∴BD⊥面SAC 即BD⊥AC BD⊥DE ∴∠EDC为所求.
设SA=a则AB=a SB=BC=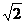 a SC=2a ∠ASC=60°
∠SCA=30° ∠EDC=60°
a SC=2a ∠ASC=60°
∠SCA=30° ∠EDC=60°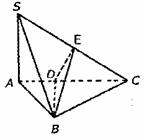
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com