
264.异面直线l1、l2,它们之间的距离为1,所成角是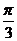 ,它们的公垂线是AB,A∈l1,B∈l2.E∈l1,F∈l2,AE=BF=1,求EF的长.
,它们的公垂线是AB,A∈l1,B∈l2.E∈l1,F∈l2,AE=BF=1,求EF的长.
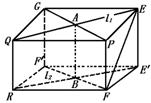
解析:如图,用异面直线l1、l2作为长方体的上、下底面的对角线,公垂线AB为高.
①EF的长即是正方形PEE′F的对角线长,为 .
.
②侧面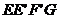 的对角线
的对角线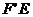 ,用勾股定理得
,用勾股定理得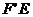 =2,即为所求.
=2,即为所求.
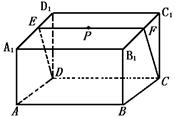
263. 在一块长方形木块的面上有一点P,木匠师傅要用锯子从P和CD将木块分成两块,问怎样画线.
解析:过P作C1D1的平行线EF,连DE、CF.
262.如果直线a垂直于直线b,那么直线a与平行于直线b的任意一条直线b′互相垂直
解析:在a上任取一点A,过A作b1∥b,则a与b1垂直.
∵b∥b′,b∥b1 ∴b1∥b′
∴直线a与b1和a与b′所成的角相等.
∴a⊥b′
261. 已知空间四边形ABCD,E、H分别是AB、AD的中点,F、G分别是边BC、DC的三等分点.
求证:①对角线AC、BD是异面直线,
②EF和HG必交于一点,且交点在AC上.
解析:①提示:用反证法,或者用判定定理.
②提示:先证EH∥FG,EH<FG,设FE∩GH=0
又
0∈GH.GH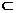 平面ADC.∴O∈平面ADC.同理O∈平面ABC.
平面ADC.∴O∈平面ADC.同理O∈平面ABC.
∴O在平面ADC和平面ABC的交线AC上.
260. .若a、b为异面直线,P为空间一点,过P且与a、b所成角均为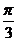 的直线有( )
的直线有( )
A.二条 B.二条或三条
C.二条或四条 D.二条、三条或四条
解析:D
259. 已知异面直线a与b所成的角为50°,P为空间一定点,则过点P且与a、b所成的角都是30°的直线有且仅有( )
A.1条 B.2条 C.3条 D.4条
解析: 过P点分别作直线a′∥a,b′∥b,则a′与b′的夹角为50°,由异面直线所成的角的定义可知,过P点与a′,b′成30°角的条数,就是所求的条数.
画图可知,过P点与a′、b′成30°角的直线只有两条.
∴ 应选B.
258. 在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是( )
A.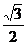 B.
B.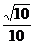 C.
C.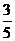 D.
D.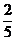
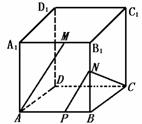
解析:由图所示,AM与CN是异面直线,过N作平行于AM的平行线NP,交AB于P,由定义可知∠PNC就是AM与CN所成的角.因ΔPBC,ΔPBN,ΔCBN皆为直角三角形,且BP=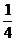 ,BN=
,BN=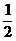 ,BC=1,故PN2=(
,BC=1,故PN2=(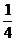 )2+(
)2+(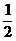 )2=
)2=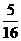 ,CN2=(
,CN2=(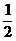 )2+12=
)2+12=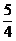 ,PC2=(
,PC2=(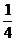 )2+12=
)2+12=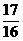 ,在ΔPCN中cos∠PNC=
,在ΔPCN中cos∠PNC=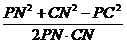 ,所以cos∠PNC=
,所以cos∠PNC=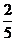 ,因此应选D.
,因此应选D.
257. 如图,ABCD-A1B1C1D1是正方体,B1E1=D1F1=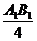 ,则BE1与DF1所成角的余弦值是( )
,则BE1与DF1所成角的余弦值是( )
A.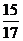 B.
B.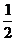 C.
C.
 D.
D.
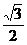

解析:过A点在平面ABB1A1内作AF,使A1F=D1F1,则ADF1F是平行四边形,∴FA∥DF1,再过E1在平面ABB1A1内作E1E∥FA,则∠BE1E即是BE1与DF1所成的角,由已知BE1=DF1=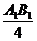 ,ABCD-A1B1C1D1是正方体,∴ E1E=
,ABCD-A1B1C1D1是正方体,∴ E1E=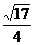 A1B1,
A1B1,
又DF1=AF=E1E,DF1=BE1.
∴
E1E=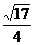 A1B1,EB=
A1B1,EB=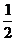 A1B1
A1B1
在ΔBE1E中,cos∠BE1E=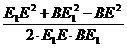 =
=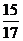 .
.
∴ 应选A.
256.分别和两条异面直线AB、CD同时相交的两条直线AC、BD一定是异面直线,为什么?
证明:假设AC、BD不异面,则它们都在某个平面α内,这时A、B、C、D四点都在α上,由公理1知A、B、C、D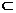 α,这与已知AB与CD异面矛盾,所以AC、BD一定是异面直线.
α,这与已知AB与CD异面矛盾,所以AC、BD一定是异面直线.
255.已知:直线a和直线b是异面直线,直线c∥a,直线b与c不相交,求证:b、c是异面直线.
证:因为b,c不相交,b、c的位置关系有b∥c或b、c异面两种可能.
假设b∥c,∵ c∥a,∴ a∥b,这与已知a,b是异面直线矛盾.
所以b与c不能平行,又b、c不相交
所以b,c是异面直线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com