
327. 如图,四边形EFGH为四面体A-BCD的一个截面,若截面为平行四边形,求证:(1)AB∥平面EFGH;(2)CD∥平面EFGH
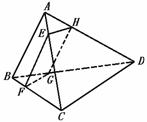
证明:(1)∵EFGH为平行四边形,∴EF∥HG,
∵HG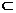 平面ABD,∴EF∥平面ABD.
平面ABD,∴EF∥平面ABD.
∵EF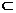 平面ABC,平面ABD∩平面ABC=AB.
平面ABC,平面ABD∩平面ABC=AB.
∴EF∥AB,∴AB∥平面EFGH.
(2)同理可证:CD∥EH,∴CD∥平面EFGH.
评析:由线线平行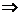 线面平行
线面平行 线线平行.
线线平行.
326. 已知正方体ABCD-A′B′C′D′中,面对角线AB′、BC′上分别有两点E、F且B′E=C′F求证:EF∥平面AC.
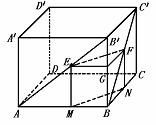
解析: 如图,欲证EF∥平面AC,可证与平面AC内的一条直线平行,也可以证明EF所在平面与平面AC平行.
证法1 过E、F分别做AB、BC的垂线EM、FN交AB、BC于M、N,连接MN
∵BB′⊥平面AC ∴ BB′⊥AB,BB′⊥BC
∴EM⊥AB,FN⊥BC
∴EM∥FN,∵AB′=BC′,B′E=C′F
∴AE=BF又∠B′AB=∠C′BC=45°
∴RtΔAME≌RtΔBNF
∴EM=FN
∴四边形MNFE是平行四边形
∴EF∥MN又MN 平面AC
平面AC
∴EF∥平面AC
证法2 过E作EG∥AB交BB′于G,连GF
∴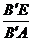 =
=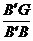
∵B′E=C′F,B′A=C′B
∴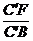 =
=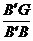 ∴FG∥B′C′∥BC
∴FG∥B′C′∥BC
又∵EG∩FG=G,AB∩BC=B
∴平面EFG∥平面AC
又EF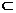 平面EFG
平面EFG
∴EF∥平面AC
325. S是空间四边形ABCD的对角线BD上任意一点,E、F分别在AD、CD上,且AE∶AD=CF∶CD,BE与AS相交于R,BF与SC相交于Q.求证:EF∥RQ.
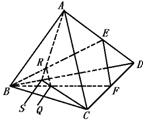
证 在ΔADC中,因AE∶AD=CF∶CD,故EF∥AC,而AC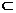 平面ACS,故EF∥平面ACS.而RQ=平面ACS∩平面RQEF,故EF∥RQ(线面平行性质定理).
平面ACS,故EF∥平面ACS.而RQ=平面ACS∩平面RQEF,故EF∥RQ(线面平行性质定理).
324. 证明:过平面上一点而与这平面的一条平行线平行的直线,在这平面上.
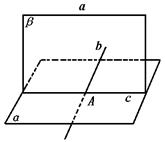
证明 如图,设直线a∥平面α,点A∈α,A∈直线b,b∥a,欲证b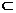 α.事实上,∵b∥a,可确定平面β,β与α有公共点A,∴α,B交于过A的直线c,∵a∥α,∴a∥c,从而在β上有三条直线,其中b、c均过点A且都与a平行.于是b、c重合,即b
α.事实上,∵b∥a,可确定平面β,β与α有公共点A,∴α,B交于过A的直线c,∵a∥α,∴a∥c,从而在β上有三条直线,其中b、c均过点A且都与a平行.于是b、c重合,即b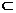 α.
α.
323. 如图,在正四棱锥S-ABCD中,P在SC上,Q在SB上,R在SD上,且SP∶PC=1∶2,SQ∶SB=2∶3,SR∶RD=2∶1.求证:SA∥平面PQR.

解析:根据直线和平面平行的判定定理,必须在平面PQR内找一条直线与AS平行即可.
证:连AC、BD,设交于O,连SO,连RQ交SO于M,取SC中点N,连ON,那么ON∥SA.
∵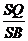 =
=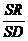 =
=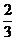
∴RQ∥BD
∴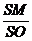 =
=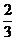 而
而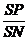 =
=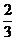
∴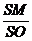 =
=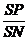 ∴PM∥ON
∴PM∥ON
∵SA∥ON.∴SA∥PM,PM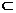 平面PQR
平面PQR
∴ SA∥平面PQR.
评析:利用平几中的平行线截比例线段定理.
三角形的中位线性质等知识促成“线线平行”向“线面平行”的转化.
322. 一直线分别平行于两个相交平面,则这条直线与它们的交线平行.
已知:α∩β=a,l∥α,l∥β.求证:l∥a.
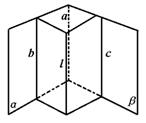
解析:由线面平行推出线线平行,再由线线平行推出线面平行,反复应用线面平行的判定和性质.
证明:过l作平面交α于b.∵l∥α,由性质定理知l∥b.
过l作平面交β于c.∵l∥β,由性质定理知l∥c.
∴
b∥c,显然c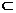 β.∴
b∥β.
β.∴
b∥β.
又
b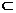 α,α∩β=a,∴
b∥a.
α,α∩β=a,∴
b∥a.
又 l∥b.
∴ l∥a.
评注:本题在证明过程中注意文字语言、符号语言,图形语言的转换和使用.
321. 如图,ABCD和ABEF均为平行四边形,M为对角线AC上的一点,N为对角线FB上的一点,且有AM∶FN=AC∶BF,求证:MN∥平面CBE.

解析:欲证MN∥平面CBE,当然还是需要证明MN平行于平面CBE内的一条直线才行.题目上所给的是线段成比例的关系,因此本题必须通过三角形相似,由比例关系的变通,才能达到“线线平行”到“线面平行”的转化.
证:连AN并延长交BE的延长线于P.
∵ BE∥AF,∴ ΔBNP∽ΔFNA.
∴
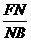 =
=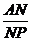 ,则
,则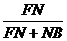 =
=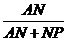 .
.
即
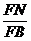 =
=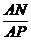 .
.
又
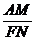 =
=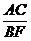 ,
,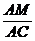 =
=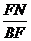 ,
,
∴
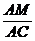 =
=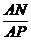 .
.
∴
MN∥CP,CP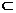 平面CBE.
平面CBE.
∴ MN∥平面CBE.
320. 已知两条异面直线a,b所成的角为θ,它们的公垂线段AA1的长度为d,在直线a、b上分别取点E、F,设A1E=m,AF=n.求证:EF=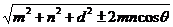
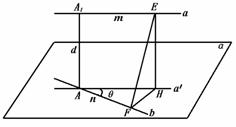
解 过A作a′∥a.
∵AA1⊥a, ∴A1A⊥a′
∴AA1⊥b,a′∩b=A
∴A1A垂直a′、b所确定的平面α.
∵a∥a′ ∴a、a′能确定平面β,在β内作EH∥A1A,交a′于H.
∵a∥a′,∴A1AME为平行四边形.
∴A1A=EH=d,AH=A1E=m
∵A1A⊥α ∴EH⊥α.
∵FH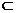 α, ∴EH⊥FH.
α, ∴EH⊥FH.
在RtΔFHE中,EF=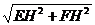 =
=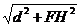
∵a′∥a ∴a′与b的夹角为θ.
即∠HAF=θ,此时AH=m,AF=n.
由余弦定理得 FH2=m2+n2-2mncosθ
∴EF=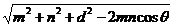
当F(或E)在A(或A1)的另一侧时,同理可得
EF=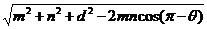 =
=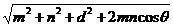
综上所述,EF=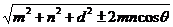
319. 已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,求点B到平面EFG的距离.
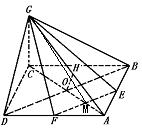
解析:注意到直线BD∥平面EFG,根据直线和平面的距离在BO中点O的距离等于B到平面EFG的距离.
解 连结AC、BD,设交于O,∵E,F分别是AB、AD的中点.
∴EF∥BD
∴BD∥平面EFG,设EF∩AC=M.
则M为OA的中点.
又AB=4 ∴AC=4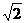 ,MO=
,MO=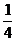 AC=
AC=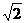 ,MC=
,MC=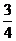 AC=3
AC=3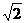
∵GC⊥平面ABCD
∴GC⊥CA,GC⊥EF
又EF⊥AC,GC∩AC=C.
∴EF⊥平面GCM.
∴过O作OH⊥GM于H,则OH⊥EF.
又OH⊥GM
故OH⊥平面EFG.
在RtΔGCM中,GM= =
=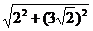 =
=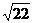 .
.
又∵OH⊥GM.∴sin∠GMC=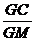 =sin∠HMO=
=sin∠HMO=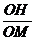 =
=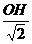
∴OH=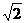 ·
·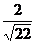 =
=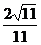
∴B点到平面GEF的距离为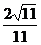
说明 本题解法甚多,学习两面垂直及简单几何体后,可用两面垂直的性质求解或者用“等体积法”求解.
318. (1)如果三棱锥S-ABC的底面是不等边三角形,侧面与底面所成的角都相等,且顶点S在底面的射影O在ΔABC内,那么O是ΔABC的( )
A.垂心 B.重心 C.外心 D.内心
(2)设P是ΔABC所在平面α外一点,若PA,PB,PC与平面α所成的角都相等,那么P在平面α内的射影是ΔABC的( )
A.内心 B.外心 C.垂心 D.重心
解 (1)利用三垂线定理和三角形全等可证明O到ΔABC的三边的距离相等,因而O是ΔABC的内心,因此选D.
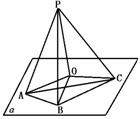
(2)如图所示,作PO⊥平面α于O,连OA、OB、OC,那么∠PAO、∠PBO、∠PCO分别是PA、PB、PC与平面α所成的角,且已知它们都相等.
∴RtΔPAO≌RtΔPBO≌RtΔPCO.
∴OA=OB=OC
∴应选B.
说明 三角形的内心、外心、垂心、旁心、重心,它们的定义和性质必须掌握.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com