50. 点A是BCD所在平面外一点，AD=BC，E、F分别是AB、CD的中点，且EF= AD，求异面直线AD和BC所成的角。(如图)　　　　　　

解析：设G是AC中点，连接DG、FG。因D、F分别是AB、CD中点，故EG∥BC且EG= BC，FG∥AD，且FG=AD，由异面直线所成角定义可知EG与FG所成锐角或直角为异面直线AD、BC所成角，即∠EGF为所求。由BC=AD知EG=GF=AD，又EF=AD_，由余弦定理可得cos∠EGF=0，即∠EGF=90°。

　　 注：本题的平移点是AC中点G，按定义过G分别作出了两条异面直线的平行线，然后在△EFG中求角。通常在出现线段中点时，常取另一线段中点，以构成中位线，既可用平行关系，又可用线段的倍半关系。

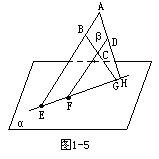
49.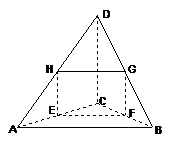 设空间四边形ABCD，E、F、G、H分别是AC、BC、DB、DA的中点，若AB＝12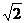，CD＝4 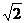，且四边形EFGH的面积为12 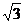，求AB和CD所成的角.

解析： 由三角形中位线的性质知，HG∥AB，HE∥CD，∴ ∠EHG就是异面直线AB和CD所成的角.

∵　 EFGH是平行四边形，HG＝ AB＝6，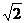

HE＝ ，CD＝2，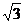

∴　 S_EFGH＝HG·HE·sin∠EHG＝12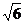 sin∠EHG,∴ 12 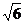sin∠EHG＝12.

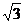∴　 sin∠EHG＝,故∠EHG＝45°.

∴　 AB和CD所成的角为45°

注：本例两异面直线所成角在图中已给，只需指出即可。

48.经过平面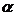外两点A，B和平面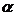垂直的平面有几个？

解析：一个或无数多个。

当A，B不垂直于平面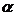时，只有一个。

当A，B垂直于平面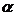时，有无数多个。

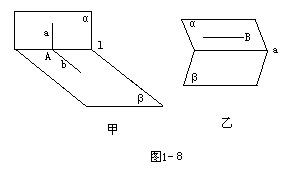
47. 画出满足下列条件的图形。

(1)α∩β=1，a 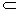α，b 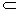β，a∩b=A

(2)α∩β=a，b 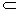β，b∥a

解析：如图1-8-甲，1-8-乙

46. 三条平行直线可以确定平面_________个。答案：1个或3个

解析：分类、一类三线共面，即确定一个平面，另一类三线不共面，每两条确定一个，可确定3个。

45. 三角形、四边形、正六边形、圆，其中一定是平面图形的有________3个。

解析：三角形的三个顶点不在一条直线上，故可确定一个平面，三角形在这个平面内；圆上任取三点一定不在一条直线上，这三点即确定一个平面，也确定了这个圆所在的平面，所以圆是平面图形；而正六边形内接于圆，故正六边形也是平面图形；而四边形就不一定是平面图形了，它的四个顶点可以不在同一平面内。

44. 空间一条直线及不在这条直线上的两个点，如果连结这两点的直线与已知直线_______，则它们在同一平面内。答案：相交或平行

解析：根据推论2，推论3确定平面的条件。

43. 如果一条直线上有一个点不在平面上，则这条直线与这个平面的公共点最多有____1个。

解析：如果有两个，则直线就在平面内，那么直线上的所有点都在这个平面内，这就与已知有一个点不在平面上矛盾，所以这条直线与这个平面的公共点最多有一个。

42. 下列命题中正确的个数是　 [　　 ]

①三角形是平面图形　 ②四边形是平面图形

③四边相等的四边形是平面图形　　 ④矩形一定是平面图形

A．1个　　 B．2个　 C．3个　 D．4个

解析：命题①是正确的，因为三角形的三个顶点不共线，所以这三点确定平面。

命题②是错误，因平面四边形中的一个顶点在平面的上、下方向稍作运动，就形成了空间四边形。命题③也是错误，它是上一个命题中比较特殊的四边形。

命题④是正确的，因为矩形必须是平行四边形，有一组对边平行，则确定了一个平面。

360.　 如图，设平面AC与平面BD相交于BC，它们所成的一个二面角为45°，P∈平面AC，Q∈平面BD，已知直线MQ是直线PQ在平面BD内的射影，且M在BC上，又直线PQ与平面BD所成的角为β，∠CMQ＝θ，0°＜θ＜90°，设线段PM＝a，求PQ的长.

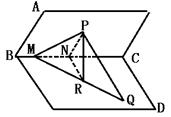
解析：在ΔPMQ中因为PM＝a,∠PQM＝β，欲求PQ的长，根据正弦定理只要能求出sin∠PMR就行了.

解　 设PMR＝α，作PR⊥MQ于R，显然PR⊥平面BD.

作RN⊥BC于N，连PN，则PN⊥BC.∴∠PNR＝45°，∠PQM＝β.

在直角ΔPMR中：PR＝asinα,MR＝acosα.

在直角ΔMNR中：NR＝MRsinθ＝acosαsinθ.

∵PR＝NR，∴asinα＝acosαsinθ.

∴tanα＝sinθ,cosα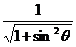＝,sinα＝.

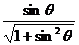在ΔPMQ中由正弦定理：

＝,

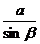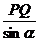∴PQ＝＝.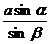

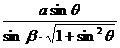评析：本题是利用正弦定理通过解斜三角形求出PQ的长，当然也可以通过三个直角三角形中的关系转换，先出求PR，最后在直角ΔPQR中利用锐角函数处理，相比之下，还是给出的解法略为简便些.