
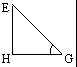
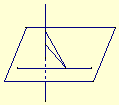
69. 如图,ABCD-A1B1C1D1是正方体,E、F分别是AD、DD1的中点,则面EFC1B和面BCC1所成二面角的正切值等于
 解析:为了作出二面角E-BC1-C的平面角,需在一个面内取一点,过该点向另一个面引垂线(这是用三垂线定理作二面角的平面角的关键步骤)。
解析:为了作出二面角E-BC1-C的平面角,需在一个面内取一点,过该点向另一个面引垂线(这是用三垂线定理作二面角的平面角的关键步骤)。 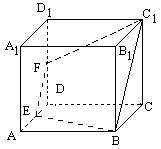
从图形特点看,应当过E(或F)作面BCC1的垂线.
解析:过E作EH⊥BC,垂足为H. 过H作HG⊥BC1,垂足为G.连EG.
∵面ABCD⊥面BCC1,而EH⊥BC
∵EH⊥面BEC1,
EG是面BCC1的斜线,HG是斜线EG在面BCC1内的射影.
∵HG⊥BC1, 
∴EG⊥BC1,
∴∠EGH是二面角E-BC1-C的平面角。
在Rt△BCC1中:sin∠C1BC=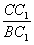 =
=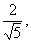 在Rt△BHG中:sin∠C1BC=
在Rt△BHG中:sin∠C1BC=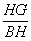 ∴HG=
∴HG=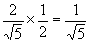 (设底面边长为1).
(设底面边长为1).
而EH=1,
在Rt△EHG中:tg∠EGH=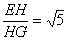 ∴∠EGH=arctg
∴∠EGH=arctg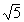 故二面角E-BC1-C 等于arctg
故二面角E-BC1-C 等于arctg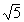 .
. 
68. m和n是分别在两个互相垂直的面α、β内的两条直线,α与β交于l,m和n与l既不垂直,也不平行,那么m和n的位置关系是 A.可能垂直,但不可能平行 B.可能平行,但不可能垂直 C.可能垂直,也可能平行 D.既不可能垂直,也不可能平行
解析:这种结构的题目,常常这样处理,先假设某位置关系成立,在此基础上进行推理,若无矛盾,且推理过程可逆,就肯定这个假设;若有矛盾,就否定这个假设。 设m//n,由于m在β外,n在β内, ∴m//β 而α过m与β交于l ∴m//l,这与已知矛盾, ∴m不平行n. 设m⊥n,在β内作直线α⊥l, ∵α⊥β, ∴a⊥α, ∴m⊥a. 又由于n和a共面且相交(若a//n 则n⊥l,与已知矛盾) ∴m⊥β, ∴m⊥l与已知矛盾, ∴m和n不能垂直. 综上所述,应选(D).
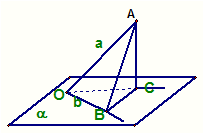
67. 直线a是平面α的斜线,b在平α内,已知a与b成60°的角,且b与a在平α内的射影成45°角时,a与α所成的角是( )
 A.45° B.60°
A.45° B.60°
C.90° D.135°
解A

66. 空间四边形ABCD中,AD=BC=2,E,F分别是AB,CD的中点,EF=√3,则AD,BC所成的角为( )
A.30° B.60°
C.90° D.120°
解B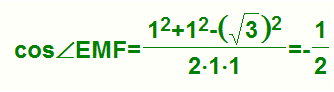 注:考察异面直线所成角的概念,范围及求法,需注意的是,异面直线所成的角不能是钝角,而利用平行关系构造可求解的三角形,可能是钝角三角形,望大家注意。同时求角的大小是先证明再求解这一基本过程。
注:考察异面直线所成角的概念,范围及求法,需注意的是,异面直线所成的角不能是钝角,而利用平行关系构造可求解的三角形,可能是钝角三角形,望大家注意。同时求角的大小是先证明再求解这一基本过程。
65..如图,空间四边形ABCD的各边及对角线长都是1,点M在边AB上运动、点Q在边CD上运动,则P、Q的最短距离为( )

解析:B
当M,N分别为中点时。
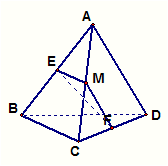 因为AB, CD为异面直线,所以M, N的最短距离就是异面直线AB,CD的距离为最短。连接BN,AN则CD⊥BN,CD⊥AN且AN=BN,所以NM⊥AB。同理,连接CM,MD可得MN⊥CD。所以MN为AB,CD的公垂线。因为AN=BN=
因为AB, CD为异面直线,所以M, N的最短距离就是异面直线AB,CD的距离为最短。连接BN,AN则CD⊥BN,CD⊥AN且AN=BN,所以NM⊥AB。同理,连接CM,MD可得MN⊥CD。所以MN为AB,CD的公垂线。因为AN=BN=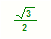 所以在RT△BMN中,MN=
所以在RT△BMN中,MN=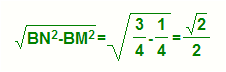 求异面直线的距离通常利用定义来求,它包括两个步骤:先证一条线段同时与两异面直线相交垂直;再利用数量关系求解。在做综合题时往往大家只重视第二步,而忽略第一步。
求异面直线的距离通常利用定义来求,它包括两个步骤:先证一条线段同时与两异面直线相交垂直;再利用数量关系求解。在做综合题时往往大家只重视第二步,而忽略第一步。
64.异面直线a、b,a⊥b,c与a成30°角,则c与b成角的范围是
( )
A. 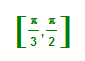 B.
B.
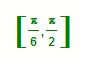
C. 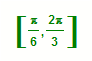 D.
D.
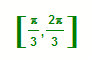
解A 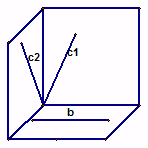 直线c在位置c2时,它与b成角的最大值为90°,直线c在c1位置时,它与b成角的最小值是60°
直线c在位置c2时,它与b成角的最大值为90°,直线c在c1位置时,它与b成角的最小值是60°
63.. 正方体ABCD-A’B’C’D’中,异面直线CD’和BC’所成的角的度数是( )
A.45° B.60°
C.90° D.120°
解析:B 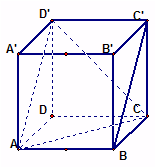
∠AD’C=60°即为异面直线CD’和BC’所成的角的度数为60°
62.在正方体ABCD-A’B’C’D’中12条棱中能组成异面直线的总对数是
( )
A.48对 B.24对
C.12对 D.6对
解析:B
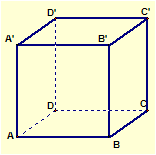 棱AA’有4条与之异面,所以,所有棱能组成4×12=48对,但每一对都重复计算一次,共有24对.
棱AA’有4条与之异面,所以,所有棱能组成4×12=48对,但每一对都重复计算一次,共有24对.
61. 在正方体ABCD-A’B’C’D’中,与棱AA’异面的直线共有几条
( )
A.4 B.6
C.8 D.10
解析:A
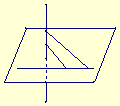
60. l1、l2是两条异面直线,直线m1、m2与l1、l2都相交,则m1、m2的位置关系是( )
A.异面或平行 B.相交
C.异面 D.相交或异面
解析:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com