
110. 已知:AB与CD为异面直线,AC=BC,AD=BD.
求证:AB⊥CD.
说明:(1)应用判定定理,掌握线线垂直的一般思路.
(2)思路:欲证线线垂直,只需证线面垂直,再证线线垂直,而由已知构造线线垂直是关键.
(3)教学方法,引导学生分析等腰三角形三线合一的性质构造图形,找到证明方法.
证明:如图,取AB中点E,连结CE、DE
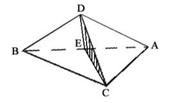 ∵AC=BC,E为AB中点.
∵AC=BC,E为AB中点.
∴CE⊥AB
同理DE⊥AB,又CE∩DE=E,
且CE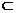 平面CDE,DE
平面CDE,DE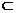 平面CDE.
平面CDE.
 ∴AB⊥平面CDE
∴AB⊥平面CDE
又CD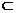 平面CDE
平面CDE
∴AB⊥CD.
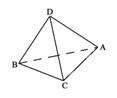
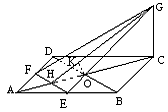
109. 已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC=2.求点B到平面EFG的距离.
解析:如图,连结EG、FG、EF、BD、AC、EF、BD分别交AC于H、O. 因为ABCD是正方形,E、F分别为AB和AD的中点,故EF∥BD,H为AO的中点.
BD不在平面EFG上.否则,平面EFG和平面ABCD重合,从而点G在平面的ABCD上,与题设矛盾.
由直线和平面平行的判定定理知BD∥平面EFG,所以BD和平面EFG的距离就是点B到平面EFG的距离. --4分
 ∵
BD⊥AC,
∵
BD⊥AC,
∴ EF⊥HC.
∵ GC⊥平面ABCD,
∴ EF⊥GC,
∴ EF⊥平面HCG.
∴ 平面EFG⊥平面HCG,HG是这两个垂直平面的交线. --6分
作OK⊥HG交HG于点K,由两平面垂直的性质定理知OK⊥平面EFG,所以线段OK的长就是点B到平面EFG的距离. --8分
∵ 正方形ABCD的边长为4,GC=2,
∴ AC=4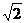 ,HO=
,HO=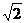 ,HC=3
,HC=3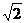 .
.
∴ 在Rt△HCG中,HG= .
.
由于Rt△HKO和Rt△HCG有一个锐角是公共的,故Rt△HKO∽△HCG.
∴ OK=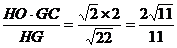 .
.
即点B到平面EFG的距离为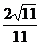 .
--10分
.
--10分
注:未证明“BD不在平面EFG上”不扣分.
108. 已知四面体S-ABC中,SA⊥底面ABC,△ABC是锐角三角形,H是点A在面SBC上的射影.求证:H不可能是△SBC的垂心.
分析:本题因不易直接证明,故采用反证法.
证明:假设H是△SBC的垂心,连结BH,并延长交SC于D点,则BH⊥SC
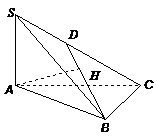 ∵
AH⊥平面SBC,
∵
AH⊥平面SBC,
∴ BH是AB在平面SBC内的射影
∴ SC⊥AB(三垂线定理)
又∵ SA⊥底面ABC,AC是SC在面内的射影
∴ AB⊥AC(三垂线定理的逆定理)
∴ △ABC是Rt△与已知△ABC是锐角三角形相矛盾,于是假设不成立.
故H不可能是△SBC的垂心.
107. 已知各棱长均为a的正四面体ABCD,E是AD边的中点,连结CE.求CE与底面BCD所成角的正弦值.
解析:作AH⊥底面BCD,垂足H是正△BCD中心,
连DH延长交BC于F,则平面AHD⊥平面BCD,
作EO⊥HD于O,连结EC,
则∠ECO是EC与底面BCD所成的角
则EO⊥底面BCD.
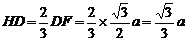
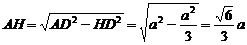
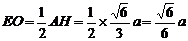 ,
,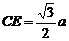
∴ 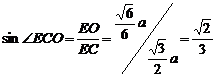
106. 已知异面直线l1和l2,l1⊥l2,MN是l1和l2的公垂线,MN = 4,A∈l1,B∈l2,AM = BN = 2,O是MN中点.① 求l1与OB的成角.②求A点到OB距离.
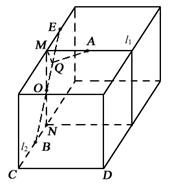 分析:本题若将条件放入立方体的“原型”中,抓住“一个平面四条线”的图形特征及“直线平面垂直”的关键性条件,问题就显得简单明了.
分析:本题若将条件放入立方体的“原型”中,抓住“一个平面四条线”的图形特征及“直线平面垂直”的关键性条件,问题就显得简单明了.
解析:(1)如图,画两个相连的正方体,将题目条件一一标在图中.
OB在底面上射影NB⊥CD,由三垂线定理,OB⊥CD,又CD∥MA,
∴ OB⊥MA 即OB与l1成90°
(2)连结BO并延长交上底面于E点.
|
∴ ME = 2,又 ON = 2
∴  .
.
作AQ⊥BE,连结MQ.
对于平面EMO而言,AM、AQ、MQ分别为垂线、斜线、斜线在平面内的射影,由三垂线逆定理得MQ⊥EO.
在Rt△MEO中,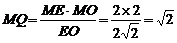 .
.
 评述:又在Rt△AMQ中,
评述:又在Rt△AMQ中,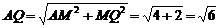 ,本题通过补形法使较困难的问题变得明显易解;求点到直线的距离,仍然是利用直线与平面垂直的关键条件,抓住“一个面四条线”的图形特征来解决的.
,本题通过补形法使较困难的问题变得明显易解;求点到直线的距离,仍然是利用直线与平面垂直的关键条件,抓住“一个面四条线”的图形特征来解决的.
105. 将矩形ABCD沿对角线BD折起来,使点C的新位置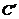 在面ABC上的射影E恰在AB上.
在面ABC上的射影E恰在AB上.
求证: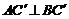
分析:欲证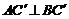 ,只须证
,只须证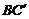 与
与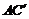 所在平面
所在平面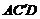 垂直;而要证
垂直;而要证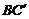 ⊥平面
⊥平面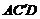 ,只须证
,只须证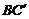 ⊥
⊥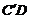 且
且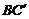 ⊥AD.因此,如何利用三垂线定理证明线线垂直就成为关键步骤了.
⊥AD.因此,如何利用三垂线定理证明线线垂直就成为关键步骤了.
证明:由题意,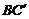 ⊥
⊥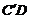 ,又斜线
,又斜线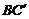 在平面ABCD上的射影是BA,
在平面ABCD上的射影是BA,
∵ BA⊥AD,由三垂线定理,得 ,
,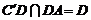 .
.
∴ 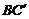 ⊥平面
⊥平面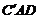 ,而
,而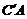
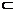 平面
平面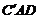
∴ 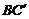 ⊥
⊥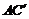
104. P是△ABC所在平面外一点,O是点P在平面α上的射影.
(1)若PA = PB = PC,则O是△ABC的____________心.
(2)若点P到△ABC的三边的距离相等,则O是△ABC_________心.
(3)若PA 、PB、PC两两垂直,则O是△ABC_________心.
(4)若△ABC是直角三角形,且PA = PB = PC则O是△ABC的____________心.
(5)若△ABC是等腰三角形,且PA = PB = PC,则O是△ABC的____________心.
(6)若PA、PB、PC与平面ABC所成的角相等,则O是△ABC的________心;
解析:(1)外心.∵ PA=PB=PC,∴ OA=OB=OC,∴ O是△ABC的外心.
(2)内心(或旁心).作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,连结PD、PE、PF.∵ PO⊥平面ABC,∴ OD、OE、OF分别为PD、PE、PF在平面ABC内的射影,由三垂线定理可知,PD⊥AB,PE⊥BC,PF⊥AC.由已知PD=PE=PF,得OD=OE=OF,∴ O是△ABC的内心.(如图答9-23)
(3)垂心.
(4)外心.(5)外心
(6)外心.PA与平面ABC所成的角为∠PAO,在△PAO、△PBO、△PCO中,PO是公共边,∠POA=∠POB=∠POC=90°,∠PAO=∠PBO=∠PCO,∴ △PAO≌△PBO≌△PCO,∴ OA=OB=OC,∴ O为△ABC的外心.
(此外心又在等腰三角形的底边高线上).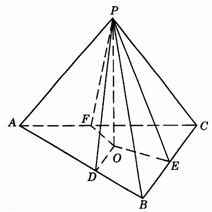
103. 已知a、b、c是平面α内相交于一点O的三条直线,而直线l和α相交,并且和a、b、c三条直线成等角.
求证:l⊥α
证法一:分别在a、b、c上取点A、B、C并使AO = BO = CO.设l经过O,在l上取一点P,在△POA、△POB、△POC中,
∵ PO公用,AO = BO = CO,∠POA =∠POB=∠POC,
∴ △POA≌△POB≌△POC
∴ PA = PB = PC.取AB中点D.连结OD、PD,则OD⊥AB,PD⊥AB,
∵ 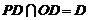
∴ AB⊥平面POD
∵ PO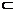 平面POD.
平面POD.
∴ PO⊥AB.
同理可证 PO⊥BC
∵ 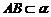 ,
,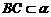 ,
,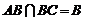
∴ PO⊥α,即l⊥α
若l不经过O时,可经过O作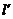 ∥l.用上述方法证明
∥l.用上述方法证明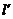 ⊥α,
⊥α,
∴ l⊥α.
证法二:采用反证法
假设l不和α垂直,则l和α斜交于O.
同证法一,得到PA = PB = PC.
过P作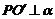 于
于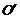 ,则
,则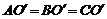 ,O是△ABC的外心.因为O也是△ABC的外心,这样,△ABC有两个外心,这是不可能的.
,O是△ABC的外心.因为O也是△ABC的外心,这样,△ABC有两个外心,这是不可能的.
∴ 假设l不和α垂直是不成立的.
∴ l⊥α
若l不经过O点时,过O作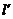 ∥l,用上述同样的方法可证
∥l,用上述同样的方法可证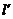 ⊥α,
⊥α,
∴ l⊥α
评述:(1)证明线面垂直时,一般都采用直接证法(如证法一),有时也采用反证法(如证法二)或同一法.
2、由于CD^平面, 把DE转化到直角三角形中求解, 从而转化为先求DE在平面内的射影长。
解: 连AC, BC, 过D作DE^AB, 连CE, 则DE为D到直线AB的距离。
∵CD^
∴AC, BC分别是AD, BD在内的射影。
∴ÐDAC, ÐDBC分别是AD和BD与平面所成的角
∴ÐDAC = 30°, ÐDBC = 45°
在Rt△ACD中,
∵CD = h, ÐDAC = 30°
∴AC =
在Rt△BCD中
∵CD = h, ÐDBC = 45°
∴BC = h
∵CD^, DE^AB
∴CE^AB
在Rt△ACB中
∴
∴在Rt△DCE中,
∴点D到直线AB的距离为。
102. 已知: 如图, △ABC中, ÐACB = 90°, CD^平面, AD, BD和平面所成的角分别为30°和45°, CD = h, 求: D点到直线AB的距离。
解析:1、先找出点D到直线AB的距离, 即过D点作 DE^AB, 从图形以及条件可知, 若把DE放在△ABD中不易求解。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com