2、如何找斜线在平面内的射影, 显然是过A点作直线垂直于平面BCD, 这样斜线与直线的位置关系, 通过射影与直线的位置关系判定。

证明:　 过A点作AO垂直于平面BCD于O

　　　　 连BO, CO, DO

　　　　 ∵AO^平面BCD, AC^BD

　　　　 ∴CO^BD

　　　　 ∵AO^平面BCD, AD^BC 　　　　　　　　　　　　　　　

　　　　 ∴DO^BC

　　　　 ∴O为△BCD的垂心

　　　　 ∴BO^CD

　　　　 ∴AB^CD

119. 在空间四边形ABCD中, 已知AC^BD, AD^BC, 求证: AB^CD。

解析：　　 1、条件AC^BD, AD^BC, 可以看作斜线AD, AC与平面BCD内的直线的位置关系, 从而联想到用三垂线定理或其逆定理证明命题。

118. 如图02，在长方体ABCD－A₁B₁C₁D₁中，P、Q、R分别是棱AA₁、BB₁、BC上的点，PQ∥AB，C₁Q⊥PR，求证：∠D₁QR=90°．

证明：∵ PQ∥AB，AB⊥平面BC₁，

∴ PQ⊥平面BC₁，QR是PR在平面BC₁的射影．

根据三垂线定理的逆定理，由C₁Q⊥PR得C₁Q⊥QR．

又因D₁C₁⊥平面BC₁，则C₁Q是D₁Q在平面B₁C的射影，根据三垂线定理，由C₁Q⊥QR得QR⊥D₁Q．

∴ ∠D₁QR=90°

117. 点P在平面ABC的射影为O，且PA、PB、PC两两垂直，那么O是△ABC的(　　 )

(A) 内心　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (B) 外心

(C) 垂心　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (D) 重心

解析：由于PC⊥PA，PC⊥PB，所以PC⊥平面PAB，

∴ PC⊥AB．

又P在平面ABC的射影为O，连CO，则CO是PC在平面ABC的射影，根据三垂线定理的逆定理，得：CO⊥AB，

同理可证AO⊥BC，O是△ABC的垂心，答案选C．

116. 已知PA⊥矩形ABCD所在平面，且AB＝3，BC＝4，PA＝3，求点P到CD和BD的距离．

解析：∵ PA⊥平面ABCD，AD⊥CD，且CD平面ABCD．

∴ PD⊥CD(三垂线定理)．在Rt△PAD中，PD＝＝＝5．

又作PH⊥BD于H，连结AH，由三垂线定理的逆定理，

有AH⊥BD．这里，PH为点P到BD的距离．

在Rt△ABD中，AH＝＝

在Rt△PAH中，PH＝＝＝

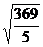
115. 已知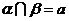：，α⊥γ，β⊥γ，b∥α，b∥β．

求证：a⊥γ且b⊥γ．

解析：在a上任取一点P，过P作PQ⊥r．

∵ β⊥r，　　　 ∴ ，

∵ α⊥r，　　　 ∴ ，

∴ PQ与a重合，故a⊥r．

过b和点P作平面S，

则S和α交于PQ₁，S和β交于PQ₂，

∵ b∥α，b∥β

∴ b∥PQ₁，且b∥PQ₂．

于是PQ₁和PQ₂与a重合，

故b∥a，　 而a⊥r，　 ∴ b⊥r．

114. α、β是两个不同的平面，m，n是平面α及β之外的两条不同直线，给出四个论断：①m⊥n，②α⊥β，③n⊥β，④m⊥α．以其中三个论断作为条件，余下的一个论断作为结论，写出你认为正确的一个命题，并证明它．

解析：m⊥α，n⊥β，α⊥β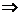m⊥n(或m⊥n，m⊥α，n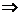⊥βα⊥β)

证明如下：过不在α、β内的任一点P，作PM∥m，PN∥n

过PM、PN作平面r交α于MQ，交β于NQ．

，

同理PN⊥NQ．

因此∠MPN+∠MQN = 180°，

故∠MQN = 90°∠MPN = 90°

即α⊥βm⊥n．

113. 如图在ΔABC中， AD⊥BC， ED=2AE， 过E作FG∥BC，　 且将ΔAFG沿FG折起，使∠A'ED=60°，求证:A'E⊥平面A'BC

解析：弄清折叠前后，图形中各元素之间的数量关系和位置关系。

解： ∵FG∥BC，AD⊥BC

∴A'E⊥FG

∴A'E⊥BC

设A'E=a，则ED=2a

由余弦定理得：

　　 A'D²=A'E²+ED²-2•A'E•EDcos60°

　　　 =3a²

∴ED²=A'D²+A'E²

∴A'D⊥A'E

∴A'E⊥平面A'BC

112. 在立体图形P－ABCD中，底面ABCD是正方形，PA⊥底面ABCD，PA＝AB，Q是PC中点．

AC，BD交于O点．

(Ⅰ)求二面角Q－BD－C的大小：

(Ⅱ)求二面角B－QD－C的大小．

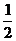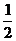解析：(Ⅰ)解：连QO，则QO∥PA且QO＝PA＝AB

∵ PA⊥面ABCD

∴ QO⊥面ABCD

面QBD过QO，

∴ 面QBD⊥面ABCD

故二面角Q－BD－C等于90°．

(Ⅱ)解：过O作OH⊥QD，垂足为H，连CH．

∵ 面QBD⊥面BCD，

又∵ CO⊥BD

CO⊥面QBD

CH在面QBD内的射影是OH

∵ OH⊥QD

∴ CH⊥QD

于是∠OHC是二面角的平面角．

设正方形ABCD边长2，

则OQ＝1，O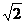D＝，QD＝．

∵ OH·QD＝OQ·OD

∴ OH＝．

又OC＝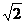

在Rt△COH中：tan∠OHC＝＝·＝

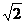∴ ∠OHC＝60°

故二面角B－QD－C等于60°．

111. 两个相交平面a、b 都垂直于第三个平面g ，那么它们的交线a一定和第三个平面垂直．

证明：在g 内取一点P，过P作PA垂直a 与g 的交线；过P作PB垂直b 与g 的交线．

∵ a⊥g 　且b⊥g

∴ PA⊥a且PB⊥b

∴ PA⊥a且PB⊥a

∴ a⊥g