5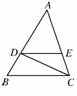．如图所示，在△ABC中，DE∥BC，＝.

求：(1)；(2).

解：(1)∵DE∥BC，

∴△ADE∽△ABC.

＝()²＝，

∴＝，则＝.

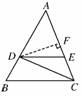(2)如图，作DF⊥AC，垂足为F.

则S_△ADE＝DF·AE，

S_△CDE＝DF·EC.

∴＝＝＝.

4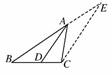．在△ABC中，AD为∠BAC的平分线，求证：＝.

证明：过C作CE∥AD，交BA的延长线于E，如图所示．

∵AD∥CE，∴＝.

又∵AD平分∠BAC，

∴∠BAD＝∠DAC，

在△BCE中，由AD∥CE知，

∠BAD＝∠E，∠DAC＝∠ACE，

∴∠ACE＝∠E，∴AE＝AC.

∴＝＝.

故＝.

3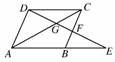．如图，在▱ABCD中，E是AB延长线上一点，DE

交AC于G，交BC于F.

求证：(1)DG²＝GE·GF；

(2)＝.

证明：(1)∵CD∥AE，

∴＝.

又∵AD∥CF，∴＝.

∴＝，即DG²＝GE·GF.

(2)∵BF∥AD，∴＝.　　　　　　　　　　　　　　　　　　　　　　　 ①

又∵CD∥BE，∴＝.　　　　　　　　　　　　　　　　　　　　　　　 ②

由①②可得＝.

2．如图，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，

连结AE，F为AE上一点，且∠BFE＝∠C.

(1)求证：△ABF∽△EAD.

(2)若AB＝4，∠1＝30°，AD＝3，求BF的长．

解：(1)证明：∵AB∥CD，∴∠1＝∠2，

又∵∠BFE＝∠C，∠BFE+∠BFA＝∠C+∠EDA

∴∠BFA＝∠ADE，∴△ABF∽△EAD.

(2)在Rt△ABE中，∠1＝30°，

由正弦定理得：＝，

∴AE＝＝，

又＝，∴BF＝·AD＝.

1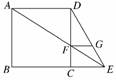．已知：如图，四边形ABCD是正方形，延长BC到点E，连结AE

交CD于F，FG∥AD交DE于G.求证：FC＝FG.

证明：在正方形ABCD中，

AB∥CD，

∴＝.

∵FG∥AD，∴＝.

∴＝.

∵AB＝AD，∴CF＝FG.

2．已知二次函数f(x)满足|f(1)|≤1，|f(0)|≤1，|f(－1)|≤1，求证：|x|≤1时，有|f(x)|≤.

证明：设f(x)＝ax²+bx+c(a≠0)，由题意，得，

∴a＝[f(1)+f(－1)－2f(0)]，b＝[f(1)－f(1)]，c＝f(0)．

代入f(x)的表达式变形得：f(x)＝f(1)(x²+x)/2+f(－1)(x²－x)/2+(1－x²)f(0)．

∵|f(1)|≤1，|f(0)|≤1，|f(－1)|≤1，∴ 当|x|≤1时，|f(x)|≤|(x²+x)/2||f(1)|+|(x²－x)/2||f(－1)|+(1－x²)|f(0)|≤|x|(1+x)/2+|x|(1－x)/2+(1－x²)＝－x²+|x|+1

＝－(|x|－1/2)²+5/4≤5/4.

1．若|a|＜1，|b|＜1，则|a+b|+|a－b|与2的大小关系是________．

解析：若(a+b)(a－b)≥0，则|a+b|+|a－b|＝|(a+b)+(a－b)|＝2|a|＜2；

若(a+b)(a－b)＜0，则|a+b|+|a－b|＝|(a+b)－(a－b)|＝2|b|＜2.∴|a+b|+|a－b|＜2.

答案：|a+b|+|a－b|＜2

10．设m等于|a|、|b|和1中最大的一个，当|x|＞m时，求证：|+|＜2.

证明：∵|x|＞m≥|a|，又|x|＞m≥|b|，且|x|＞m≥1，则|x|²＞|b|.

∴|+|≤||+||＝+＜+＝2，

故原不等式成立．

9．关于实数x的不等式|x－|≤与x²－3(a+1)x+2(3a+1)≤0(其中a∈R)的解集依次记为A与B，求使A⊆B的a的取值范围．

解答：简化集合A和B，然后对字母参数a进行讨论．

A＝{x|2a≤x≤a²+1}，B＝{x|(x－2)[x－(3a+1)]≤0}．

当3a+1≥2，即a≥时，得B＝{x|2≤x≤3a+1}．

欲使A⊆B，只要得1≤a≤3；

当3a+1＜2，即a＜时，得B＝{x|3a+1≤x≤2}．

欲使A⊆B，只要得a＝－1.

综上，使A⊆B的a的取值范围是1≤a≤3或a＝－1.

8．设f(x)＝x²－x+b，|x－a|＜1，求证：|f(x)－f(a)|＜2(|a|+1)．

证明：∵f(x)－f(a)＝(x－a)(x+a－1)，又|x－a|＜1，∴|f(x)－f(a)|＝|x－a||x+a－1|≤|x+a－1|＝|x－a+2a－1|≤|x－a|+2|a|+1＜2|a|+2＝2(|a|+1)．