
1.知识与技能
了解指数函数模型的实际背景,理解指数函数的概念,掌握指数函数的图象.
2.在学生掌握了有理指数幂的运算性质后,进一步推广到实数范围内.由此让学生体会发现规律,并由特殊推广到一般的研究方法.
发现教学法
1.经历由利用根式的运算性质对根式的化简,注意发现并归纳其变形特点,进而由特殊情形归纳出一般规律.
2.教学难点:分数指数幂概念的理解
1.教学重点:(1)分数指数幂的理解;
(2)掌握并运用分数指数幂的运算性质;
3.情感、态度与价值观
(1)培养学生观察分析,抽象的能力,渗透“转化”的数学思想;
(2)通过运算训练,养成学生严谨治学,一丝不苟的学习习惯;
(3)让学生体验数学的简洁美和统一美.
2.过程与方法
通过与初中所学的知识进行类比,得出分数指数幂的概念,和指数幂的性质.
1.知识与技能
(1)理解分数指数幂的概念;
(2)掌握分数指数幂和根式之间的互化;
(3)掌握分数指数幂的运算性质;
(4)培养学生观察分析、抽象等的能力.
教学 环节 |
教学内容 |
师生互动 |
设计意图 |
复习 引入 |
复习 1.分数指数幂的概念.  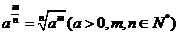  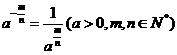  2.分数指数幂的运算性质.  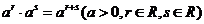  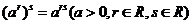  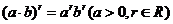 |
师:提出问题 生:复习回顾  师:总结完善 |
复习旧知,为新课作铺垫. |
应用 举例 |
例1.(P56,例4)计算下列各式(式中字母都是正数) (1) 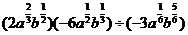  (2)     例2.(P57 例5)计算下列各式 (1) 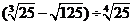 (2) 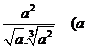 >0) >0)课堂练习: 化简: (1) 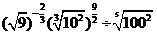 ; ;(2) 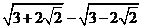 ; ;(3) 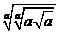 . . |
学生思考,口答,教师板演、点评. 例1 (先由学生观察以上两个式子的特征,然后分析、提问、解答) 分析:四则运算的顺序是先算乘方,再算乘除,最后算加减,有括号的先算括号的. 整数幂的运算性质及运算规律扩充到分数指数幂后,其运算顺序仍符合我们以前的四则运算顺序. 我们看到(1)小题是单项式的乘除运算;(2)小题是乘方形式的运算,它们应让如何计算呢? 其实,第(1)小题是单项式的乘除法,可以用单项式的运算顺序进行. 第(2)小题是乘方运算,可先按积的乘方计算,再按幂的乘方进行计算. 解:(1)原式 = 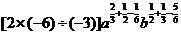 = 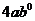 =4 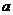 (2)原式= 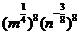 = 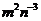 例2 分析:在第(1)小题中,只含有根式,且不是同类根式,比较难计算,但把根式先化为分数指数幂再计算,这样就简便多了,同样,第(2)小题也是先把根式转化为分数指数幂后再由运算法则计算. 解:(1)原式= 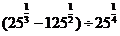 = 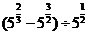 = 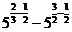 = 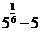 = 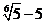 (2)原式 = 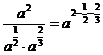 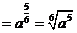 . .小结:运算的结果不强求统一用哪一种形式表示,但不能同时含有根号和分数指数,也不能既有分母,又含有负指数. 练习答案: 解(1)原式= 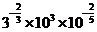 = 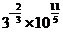 ; ;(2)原式= 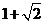 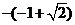 =2; (3)原式= 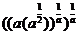 = 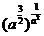 = =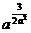 . . |
通过这二个例题的解答,巩固所学的分数指数幂与根式的互化,以及分数指数幂的求值,提高运算能力. 强化解题技巧. |
|
归纳 总结 |
1.熟练掌握有理指数幂的运算法则,化简的基础. 2.含有根式的式子化简,一般要先把根式转化为分数指数幂后再计算. |
先让学生回顾反思,然后师生共同总结,完善. |
巩固本节学习成果,形成知识体系. |
|
课后 作业 |
作业:2.1 第三课时 习案 |
学生独立完成 |
巩固新知 提升能力 |
备选例题
例1 已知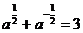 ,求下列各式的值.
,求下列各式的值.
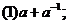
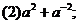
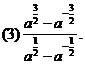
[分析]从已知条件中解出a的值,然后再代入求值,这种方法是不可取的,而应设法从整体寻求结果与条件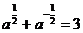 的联系,进而整体代入求值.
的联系,进而整体代入求值.
[解析](1)将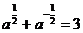 两边平方,
两边平方,
得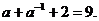
即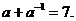
(2)将上式平方,有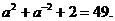
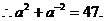
(3)由于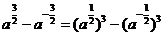
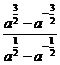
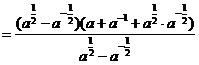
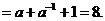
[小结]对“条件求值”问题一定要弄清已知与未知的联系,然后采取“整体代换”或“求值后代换”两种方法求值.
例2 化简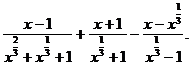
[分析]根据本题的特点,须注意到
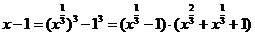 ,
,
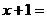
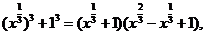
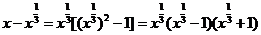 ,
,
应对原式进行因式分解.
[解析]原式
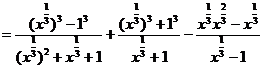
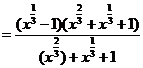
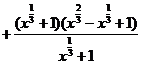
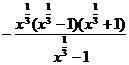
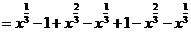
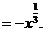
[小结]解这类题,要注意运用下列公式:
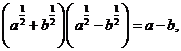
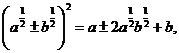
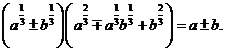
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com