
19.解:法一 :以A点为原点,AB为x轴,AD为y轴,AD为z轴的空间直角坐标系,
则依题意可知相关各点的坐标分别是A(0,0,0),B(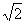 ,0,0),C(
,0,0),C(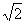 ,1,0),
,1,0),
D(0,1,0),S(0,0,1) ……………………2分
……………………2分
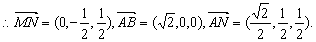 …………………………4分
…………………………4分
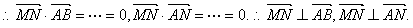
∴MN⊥平面ABN.……………………………………………………………………6分
(2)设平面NBC的法向量 且又易知
且又易知
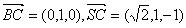
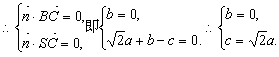
令a=1,则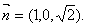 …………………………………………………………9分
…………………………………………………………9分
显然,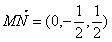 就是平面ABN的法向量.
就是平面ABN的法向量.
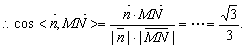 ………………………………………10分
………………………………………10分
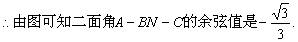 ………………………………………12分
………………………………………12分
法二:(1)由题意知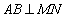 连
连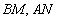 则可求
则可求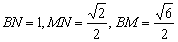 ,
,
则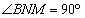
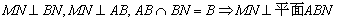 ……………6分
……………6分
(2)因为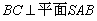 ,在平面
,在平面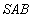 内作
内作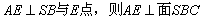 且
且 ,
,
又在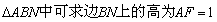 ,所以
,所以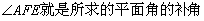 ,
,
且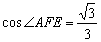 故所求的二面角的余弦值为
故所求的二面角的余弦值为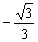 ………………………12分
………………………12分
18.解:设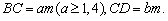 连结BD.
连结BD.
则在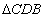 中,
中,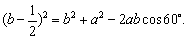
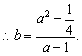
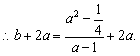 ………………………………6分
………………………………6分
设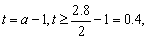

则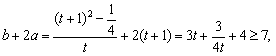 ………………………………10分
………………………………10分
等号成立时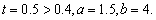 ……………………………………………11分
……………………………………………11分
答:当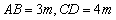 时,建造这个支架的成本最低. ……………………12分
时,建造这个支架的成本最低. ……………………12分
13:3
14: 120 15: 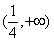 16: ③④
16: ③④ 
1--5 C A D A D 6--10 A D A C B 11 C 12 C
22.已知函数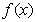 与
与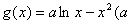 为常数)的图象关于直线x=1对称,
为常数)的图象关于直线x=1对称,
且x=1是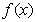 的一个极值点.
的一个极值点. 
(1)求出函数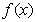 的表达式和单调区间;
的表达式和单调区间;
(2)若已知当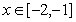 时,不等式
时,不等式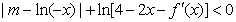 恒成立,
恒成立,
求m的取值范围.
高三9月份月考数学试卷答案及评分标准
20.某研究机构准备举行一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
|
版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
|
人数 |
20 |
15 |
5 |
10 |
(1)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(2)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为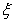 ,求随机变量
,求随机变量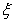 的分布列和数学期望。
的分布列和数学期望。


19.如图所示,已知四棱锥S-ABCD的底面ABCD是矩形,M、N分别是CD、SC的中点,
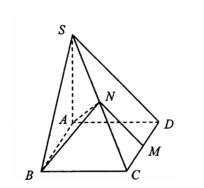
SA⊥底面ABCD,SA=AD=1,AB=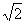 .
. 
(1)求证:MN⊥平面ABN;
(2)求二面角A-BN-C的余弦值.

18.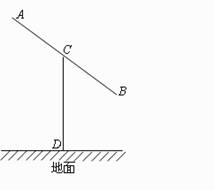 某建筑的金属支架如图所示,根据要求
某建筑的金属支架如图所示,根据要求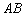 至少长2.8m,
至少长2.8m, 为
为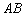 的中点,
的中点,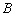 到
到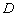 的距离比
的距离比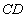 的长小0.5m,
的长小0.5m,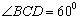 ,已知建造支架的材料每米的价格一定,问怎样设计
,已知建造支架的材料每米的价格一定,问怎样设计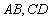 的长,可使建造这个支架的成本最低?
的长,可使建造这个支架的成本最低? 
解答应写出文字说明,证明过程或演算步骤.
17.已知△ABC的面积S满足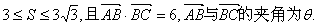
(I)求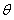 的取值范围;
的取值范围;
(2)求函数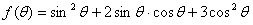 的最大值.
的最大值. 
16.给出下列命题: 
①若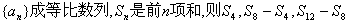 成等比数列;
成等比数列;
②已知函数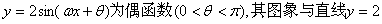 的某两个交点的横坐标为
的某两个交点的横坐标为 ;
;
③函数 至多有一个交点;
至多有一个交点;
④函数

其中正确命题的序号是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com