
4.求导数的方法
(1) 八个基本求导公式
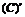 = ;
= ; 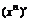 = ;(n∈Q)
= ;(n∈Q)
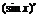 = ,
= ,
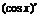 =
=
 =
,
=
,
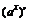 =
=
 = ,
= , 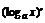 =
=
(2) 导数的四则运算
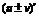 =
=
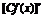 =
=
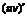 =
,
=
,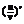 =
=
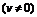
(3) 复合函数的导数
设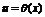 在点x处可导,
在点x处可导, 在点
在点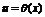 处可导,则复合函数
处可导,则复合函数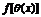 在点x处可导, 且
在点x处可导, 且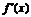 =
,即
=
,即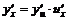 .
.
|
例1.求函数y=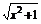 在x0到x0+Δx之间的平均变化率.
在x0到x0+Δx之间的平均变化率.
解 ∵Δy=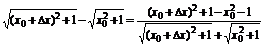
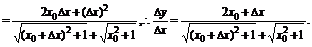
变式训练1. 求y=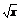 在x=x0处的导数.
在x=x0处的导数.
解 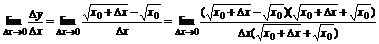
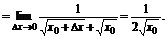
例2. 求下列各函数的导数:
(1)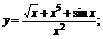 (2)
(2)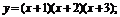
(3)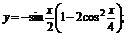 (4)
(4)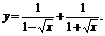
解 (1)∵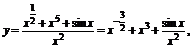
∴y′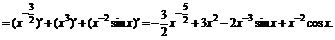
(2)方法一 y=(x2+3x+2)(x+3)=x3+6x2+11x+6,∴y′=3x2+12x+11.
方法二 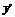 =
=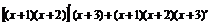
=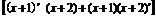 (x+3)+(x+1)(x+2)
(x+3)+(x+1)(x+2)
=(x+2+x+1)(x+3)+(x+1)(x+2)=(2x+3)(x+3)+(x+1)(x+2)=3x2+12x+11.
(3)∵y=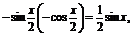
∴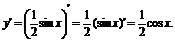
(4)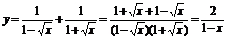 ,
,
∴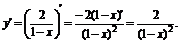
变式训练2:求y=tanx的导数.
解 y′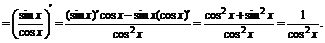
例3. 已知曲线y=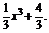
(1)求曲线在x=2处的切线方程;
(2)求曲线过点(2,4)的切线方程.
解 (1)∵y′=x2,∴在点P(2,4)处的切线的斜率k=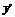 |x=2=4.
|x=2=4.
∴曲线在点P(2,4)处的切线方程为y-4=4(x-2),即4x-y-4=0.
(2)设曲线y=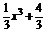 与过点P(2,4)的切线相切于点
与过点P(2,4)的切线相切于点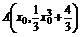 ,
,
则切线的斜率k=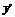 |
|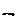 =
=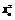 .
.
∴切线方程为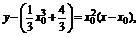 即
即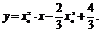
∵点P(2,4)在切线上,∴4=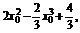
即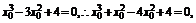 ∴
∴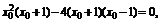
∴(x0+1)(x0-2)2=0,解得x0=-1或x0=2,
故所求的切线方程为4x-y-4=0或x-y+2=0.
变式训练3:若直线y=kx与曲线y=x3-3x2+2x相切,则k= .
答案  2或
2或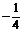
例4. 设函数 (a,b∈Z),曲线
(a,b∈Z),曲线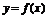 在点
在点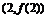 处的切线方程为y=3.
处的切线方程为y=3.
(1)求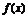 的解析式;
的解析式;
(2)证明:曲线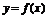 上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值,并求出此定值.
上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值,并求出此定值.
(1)解 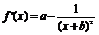 ,
,
于是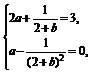 解得
解得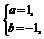 或
或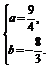
因为a,b Z,故
Z,故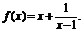
(2)证明 在曲线上任取一点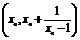 .
.
由 知,过此点的切线方程为
知,过此点的切线方程为
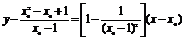 .
.
令x=1,得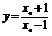 ,切线与直线x=1交点为
,切线与直线x=1交点为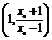 .
.
令y=x,得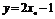 ,切线与直线y=x的交点为
,切线与直线y=x的交点为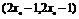 .
.
直线x=1与直线y=x的交点为(1,1).
从而所围三角形的面积为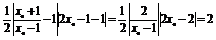 .
.
所以,所围三角形的面积为定值2.
变式训练4:偶函数f(x)=ax4+bx3+cx2+dx+e的图象过点P(0,1),且在x=1处的切线方程为y=x-2,求y=f(x)的解析式.
解 ∵f(x)的图象过点P(0,1),∴e=1. ①
又∵f(x)为偶函数,∴f(-x)=f(x).
故ax4+bx3+cx2+dx+e=ax4-bx3+cx2-dx+e.
∴b=0,d=0. ②
∴f(x)=ax4+cx2+1.
∵函数f(x)在x=1处的切线方程为y=x-2,∴可得切点为(1,-1).
∴a+c+1=-1. ③
∵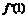 =(4ax3+2cx)|x=1=4a+2c,∴4a+2c=1. ④
=(4ax3+2cx)|x=1=4a+2c,∴4a+2c=1. ④
由③④得a=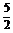 ,c=
,c=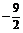 . ∴函数y=f(x)的解析式为
. ∴函数y=f(x)的解析式为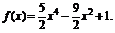
|
3.导数的几何意义:设函数y=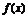 在点
在点 处可导,那么它在该点的导数等于函数所表示曲线在相应点
处可导,那么它在该点的导数等于函数所表示曲线在相应点 处的
.
处的
.
2.导函数:函数y=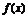 在区间(a, b)内
的导数都存在,就说
在区间(a, b)内
的导数都存在,就说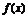 在区间( a, b )内
,其导数也是(a ,b )内的函数,叫做
在区间( a, b )内
,其导数也是(a ,b )内的函数,叫做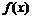 的
,记作
的
,记作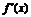 或
或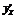 ,函数
,函数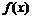 的导函数
的导函数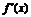 在
在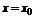 时的函数值
,就是
时的函数值
,就是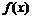 在
在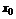 处的导数.
处的导数.
1.导数的概念:函数y=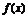 的导数
的导数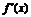 ,就是当Δ
,就是当Δ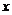
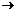 0时,函数的增量Δy与自变量的增量Δ
0时,函数的增量Δy与自变量的增量Δ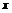 的比
的比 的
,即
的
,即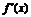 =
=
.
=
=
.
3.理解可导函数的单调性与其导数的关系;了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号);会求一些实际问题(一般指单峰函数)的最大值和最小值.
|

|
导数的应用价值极高,主要涉及函数单调性、极大(小)值,以及最大(小)值等,遇到有关问题要能自觉地运用导数.
第1课时 变化率与导数、导数的计算
|
2. 熟记八个基本导数公式(c,
熟记八个基本导数公式(c,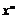 (m为有理数),
(m为有理数),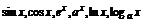 的导数);掌握两个函数和、差、积、商的求导法则,了解复合函数的求导法则,会求某些简单函数的导数.
的导数);掌握两个函数和、差、积、商的求导法则,了解复合函数的求导法则,会求某些简单函数的导数.
1. 了解导数概念的某些实际背景(如瞬时速度,加速度,光滑曲线切线的斜率等);掌握函数在一点处的导数的定义和导数的几何意义;理解导函数的概念.
了解导数概念的某些实际背景(如瞬时速度,加速度,光滑曲线切线的斜率等);掌握函数在一点处的导数的定义和导数的几何意义;理解导函数的概念.
22.解:(1)设P(x,y)是函数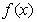 的图象上任意一点,则容易求得P点关于直线x=1的对称点为
的图象上任意一点,则容易求得P点关于直线x=1的对称点为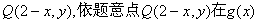 的图象上,
的图象上,
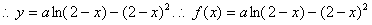 .………………2分
.………………2分
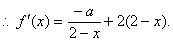
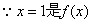 的一个极值点,
的一个极值点,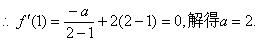
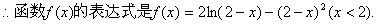 ………………4分
………………4分
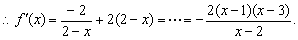

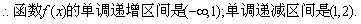 …………6分
…………6分
(2)由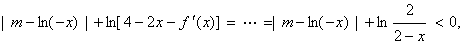
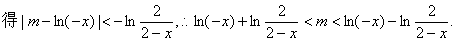 ……10分
……10分
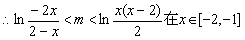 时恒成立.
时恒成立. 
 时的最小值,
时的最小值,
即可求得m的取值范围.
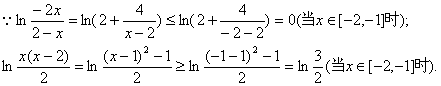
 ……………………………………………………14分
……………………………………………………14分
21.解:(Ⅰ)设椭圆的半焦距为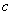 ,依题意
,依题意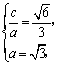
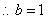 ,
, 所求椭圆方程为
所求椭圆方程为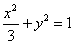 ---6分
---6分
(Ⅱ)设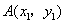 ,
,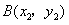 .(1)当
.(1)当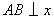 轴时,
轴时,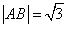 . -------------------8分
. -------------------8分
(2)当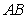 与
与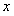 轴不垂直时,设直线
轴不垂直时,设直线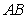 的方程为
的方程为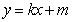 .由已知
.由已知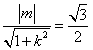 ,---------9分
,---------9分
得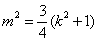 .---------10分
.---------10分
把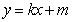 代入椭圆方程,整理得
代入椭圆方程,整理得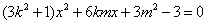 ,
,
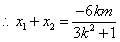 ,
,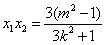 .
.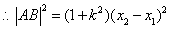
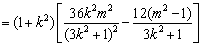
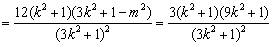

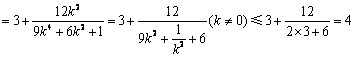 .
.
当且仅当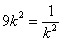 ,即
,即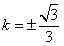 时等号成立.当
时等号成立.当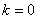 时,
时,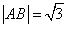 ,综上所述
,综上所述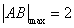 .
.
 当
当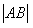 最大时,
最大时,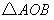 面积取最大值
面积取最大值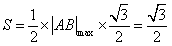 .---------------12分
.---------------12分
20.解:(1)从50名教师随机选出2名的方法数为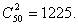
选出2人使用版本相同的方法数为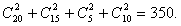
故2人使用版本相同的概率为: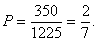 …………………………6分
…………………………6分
(2)∵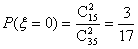 ,
,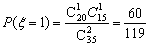
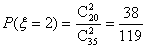
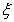 |
0 |
1 |
2 |
|
P |
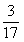 |
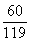 |
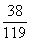 |
∴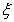 的分布列为……………10分
的分布列为……………10分
∴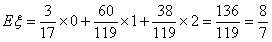 ……………………12分
……………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com