第一节：语法和词汇知识(共15小题；每小题1分，满分15分)

　　　　 从A、B、C、D四个选项中，选出可以填入空白处的最佳选项，并在答题卡上将该项涂黑。

21．-See the gathering clouds outside? Please take this umbrella with you．

　　　　 -　　 　.

　　　　 A．Thanks．Take it easy　　　　　　　　　　　　　　　　　　 B．OK, just in case

　　　　 C．Well, it just depends　　　　　　　　　　　　　　　　　　　 D．All right．I'll try my luck

2． 如图为一个几何体的三视图，尺寸如图所示，则该几何体的表面积为(不考虑接触点)(　)

A．6+ +π　 　　　　　　　 B．18+ +4π

C．18+2 +π　 　　　　　 D．32+π

解析：该几何体是正三棱柱上叠放一个球．

答案：C

1．找出与下列几何体对应的三视图，在三视图的横线上填上对应的序号．

答案：(3)　(4)　(6)　(1)　(8)　(5)　(2)　(7)

10．圆台的一个底面周长是另一个底面周长的3倍，轴截面的面积等于392 cm²，母线与轴的夹角是45°，求这个圆台的高、母线长和两底面半径．

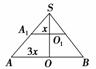
解答：圆台的轴截面如上图所示，设圆台上下底面半径分别为x cm,3x cm.延长AA₁交OO₁的延长线于S，

在Rt△SOA中，∠ASO＝45°，则∠SAO＝45°，

∴SO＝AO＝3x，∴OO₁＝2x，

又S_轴截面＝(6x+2x)·2x＝392，∴x＝7.

故圆台的高OO₁＝14 cm，母线长l＝O₁O＝14 cm，两底面半径分别为7 cm,21 cm.

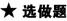
9．正四棱锥的高为，侧棱长为，求侧面上斜高(棱锥侧面三角形的高)为多少？

解答：如下图所示，正棱锥S-ABCD中高OS＝，

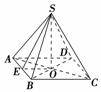
侧棱SA＝SB＝SC＝SD＝，

在Rt△SOA中，OA＝＝2，∴AC＝4.

∴AB＝BC＝CD＝DA＝2.

作OE⊥AB于E，则E为AB中点．连接SE，则SE即为斜高，则SO⊥OE.

在Rt△SOE中，

∵OE＝BC＝，SO＝，∴SE＝，即侧面上的斜高为.

8．正四棱台AC₁的高是17 cm，两底面的边长分别是4 cm和16 cm，求这个棱台的侧棱长和斜高．

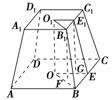
解答：如上图所示，设棱台的两底面的中心分别是O₁、O，B₁C₁和BC的中点分别是E₁和E，连接O₁O、E₁E、O₁B₁、OB、O₁E₁、OE，则四边形OBB₁O₁和OEE₁O₁都是直角梯形．

∵A₁B₁＝4 cm，AB＝16 cm，∴O₁E₁＝2 cm，OE＝8 cm，

O₁B₁＝2 cm，OB＝8 cm，

∴B₁B²＝O₁O²+(OB－O₁B₁)²＝361 cm²，E₁E²＝O₁O²+(OE－O₁E₁)²＝325 cm²，

∴B₁B＝19 cm，E₁E＝5 cm.

答：这个棱台的侧棱长为19 cm，斜高为5 cm.

7．用小正方体搭成一个几何体，右图是它的正(主)视图和侧(左)视图，搭成这个几何体的小正方体最多为________个．

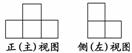
解析：画出其几何体图形，可知最多需要7个小正方体．

答案：7

6．一个几何体的三视图如图所示，则该几何体的体积等于________．

解析：三视图对应的几何体是一个棱长为2的正方体上面摆放了一个直径为2的球，因此此几何体的体积为V＝V_球+V_正方体＝π+8

答案：8+