3．溶有NaBr、KI的溶液中，通入足量氯气充分反应，然后将所得溶液蒸干灼烧，所得固体为　

A. Br₂　　　　　　　　　　　 B.I₂和KCl

　C．I₂、KCl和NaCl　　　　　 D．KCl和NaCl

2．新型环保出租车采用PLG+汽油的双燃料系统，其尾气中的有毒气体成分较普通车型下降80%左右，解决了汽车尾气排放给城市环境造成的污染问题。下列物质中不属于上述有害气体的是

　　　 A．CO₂和H₂　　 　　　　　　　　　　　　　 B．NO₂和NO　

C．CO和SO₂　 　　　　　　　　　　　　　 D．碳粒和含铅化合物　 　

1．卤族元素随着核电荷数的增加，下列叙述不正确的是

A. 元素的非金属性逐渐减弱　　　 B. 原子半径逐渐增大

C. 单质的氧化性逐渐减弱　　　　 D．氢化物的稳定性逐渐增强

1在△ABC中，,则k为(　　 )　

A2R　　　 BR　　　　　　 C4R　　　 D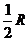(R为△ABC外接圆半径)

2△ABC中，sin²A=sin²B+sin²C，则△ABC为(　　 )　

A直角三角形?　 B等腰直角三角形　C等边三角形　 D等腰三角形

3在△ABC中，sinA＞sinB是A＞B的

A充分不必要条件 B必要不充分条件 C充要条件 D既不充分也不必要条件

4在△ABC中，求证：

例1 已知在

解：

∴

由得　

由得

例2 在

解：∵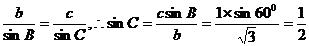

∴

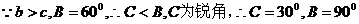
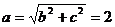
例3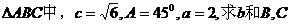

解：

，

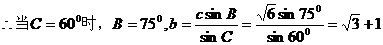例4 已知△ABC，BD为B的平分线，求证：AB∶BC＝AD∶DC

分析：前面大家所接触的解三角形问题是在一个三角形内研究问题，而B的平分线BD将△ABC分成了两个三角形：△ABD与△CBD，故要证结论成立，可证明它的等价形式：AB∶AD＝BC∶DC，从而把问题转化到两个三角形内，而在三角形内边的比等于所对角的正弦值的比，故可利用正弦定理将所证继续转化为，再根据相等角正弦值相等，互补角正弦值也相等即可证明结论

证明：在△ABD内，利用正弦定理得：

在△BCD内，利用正弦定理得：

∵BD是B的平分线

∴∠ABD＝∠DBC　 ∴sinABD＝sinDBC

∵∠ADB+∠BDC＝180°

∴sinADB＝sin(180°－∠BDC)＝sinBDC

∴

∴

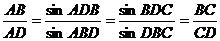
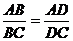
评述：此题可以启发学生利用正弦定理将边的关系转化为角的关系，并且注意互补角的正弦值相等这一特殊关系式的应用

2．两边和其中一边对角，求另一边的对角，进而可求其它的边和角(见图示)已知a, b和A, 用正弦定理求B时的各种情况:

⑴若A为锐角时:

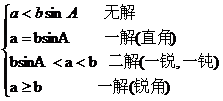
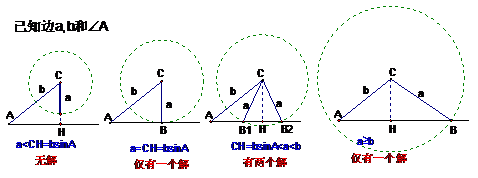
⑵若A为直角或钝角时:

1．两角和任意一边，求其它两边和一角；

正弦定理：在任一个三角形中，各边和它所对角的正弦比相等，

即　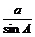==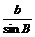 =2R(R为△ABC外接圆半径)

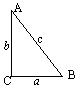　1．直角三角形中：sinA= 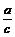，sinB=， sinC=1　

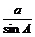即　c=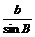， c= ，　 　c=．　　　　

∴==

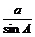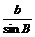2．斜三角形中

证明一：(等积法)在任意斜△ABC当中

S_△ABC=

　两边同除以即得：==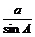

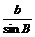证明二：(外接圆法)

如图所示，∠A＝∠D

∴

同理 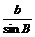=2R，＝2R

证明三：(向量法)

过A作单位向量垂直于

由　+=　　　

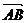
两边同乘以单位向量 得 •(+)=•

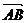
则•+•=•

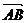
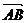∴||•||cos90°+||•||cos(90°-C)=||•||cos(90°-A)

∴　 ∴=

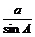同理，若过C作垂直于得： =　 ∴==

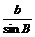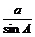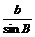正弦定理的应用 从理论上正弦定理可解决两类问题：

--提出课题：正弦定理、余弦定理

第二节　 写作 (满分30分)

　　　　 根据以上图片写一篇英语文章描述图片内容，并包括如下内容要点：