
6.转化为基本量a1,q, an=2n-1或an=23-n.
4.通项an=23n-2,f(n)是前n+4项的和; 5. 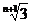
6. 已知等比数列{an}中,a1+a2+a3=7,a1a2a3=8,则通项公式为
简答:1-4.DBCD; 2.由题意得(1+r)3<1+3q,故q>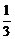 [(1+r)3-1];
[(1+r)3-1];
5. 在2与6之间插入n个数,使它们组成等比数列,则这个数列的公比为
4.(2006北京)设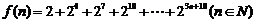 ,则
,则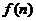 等于( )
等于( )
(A)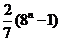 (B)
(B)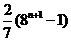 (C)
(C)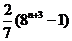 (D)
(D)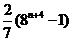
3.(2006辽宁)在等比数列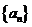 中,
中,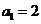 ,前
,前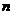 项和为
项和为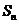 ,若数列
,若数列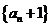 也是等比数列,则Sn等于
( )
也是等比数列,则Sn等于
( )
(A)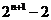 (B)
(B) (C)
(C) 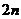 (D)
(D)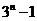
2.银行一年定期的年利率为r,三年定期的年利率为q,银行为吸收长期资金,鼓励储户存三年定期的存款,那么q的值应略大于 ( )
A.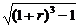 B.
B.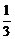 [(1+r)3-1] C.(1+r)3-1
D.r
[(1+r)3-1] C.(1+r)3-1
D.r
1.(2006湖北)若互不相等的实数a、b、c成等差数列,c、a、b成等比数列,且a+3b+c=10,则a= ( )
A.4 B.2 C.-2 D.-4
7.解等比数列题的常见思维方法
(1)方程的思想(“知三求二”问题) ;
(2)转化化归思想; 化归为等比数列,转化为基本量;
(3)分类的思想:q=1和q≠1; 由an+1-an=a1qn-1(q-1)讨论增减等.
(4)等比数列中,次数较高时,常作同除.
6.证明数列为等比数列的方法:
(1)定义法:若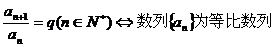
(2)等比中项法:若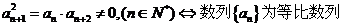
(3)通项法:若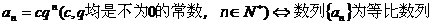
(4)前n项和法:若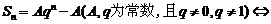 数列
数列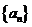 为等比数列。
为等比数列。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com