
2.叠氮酸(HN3)与醋酸酸性相近,其盐稳定,但撞击时会发生爆炸生成氮气。有关叠氮酸的叙述中正确的是
①NaN3 的水溶液呈碱性 ② HN3 的固体属于共价化合物
③NaN3 的固体属于离子化合物 ④NaN3可用于小汽车防撞保护气囊
A、①②③ B、②③④ C、①③④ D、①②③④
1、生活中碰到的某些问题,常涉及到化学知识,下列分析不正确的是
A、Mg(OH)2和Al(OH)3热分解生成的气态水可覆盖火焰、驱逐O2、稀释可燃气体,分解产物MgO和Al2O3能较快地与塑料燃烧过程中产生的酸性及腐蚀性气体反应,所以它们可以作为未来发展方向的无机阻燃剂。
B、用灼烧并闻气味的方法区别纯棉织物和纯毛织物。
C、某雨水样品采集后放置一段时间,pH值由4.68变为4.28,是因为水中溶解了较多的CO2。
D、蒙古牧民喜欢用银器盛放鲜牛奶有其科学道理:用银器盛放鲜牛奶,溶入的极微量的银离子,可杀死牛奶中的细菌,防止牛奶变质。
81、(山西大学附中2008届二月月考)设函数 (其中
(其中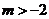 )的图象在
)的图象在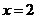 处的切线与直线
处的切线与直线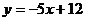 平行.
平行.
(1)求 的值;
的值;
(2)求函数 在区间[0,1]的最小值;
在区间[0,1]的最小值;
(3)若 ,
,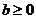 ,
,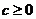 ,且
,且 ,
,
试根据上述(Ⅰ)、(Ⅱ)的结论证明: .
.
解:(1)因为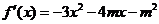 , 所以
, 所以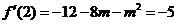
解得m=-1或m=-7(舍),即m=-1 (2)由 ,解得
,解得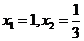
列表如下:
|
x |
0 |
(0, ) ) |
 |
( ,1) ,1) |
1 |
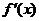 |
|
- |
|
+ |
|
|
f(x) |
2 |
↘ |
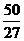 |
↗ |
2 |
所以函数 在区间[0,1]的最小值为
在区间[0,1]的最小值为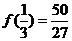
(3)因为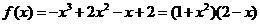
由(2)知,当x∈[0,1]时, 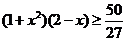 ,所以
,所以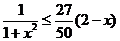 ,
,
所以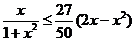
当 ,
,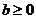 ,
,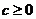 ,且
,且 时,
时, 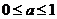 ,
,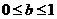 ,
,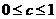 ,所以
,所以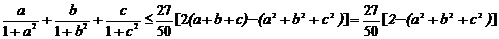
又因为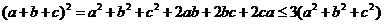 ,
,
所以
故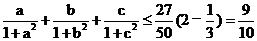 (当且仅当
(当且仅当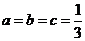 时取等号)
时取等号)
80、(山东省郓城一中2007-2008学年第一学期期末考试)已知函数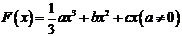 且
且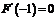
(1)若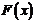 在
在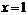 取得极小值-2,求函数
取得极小值-2,求函数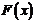 的单调区间
的单调区间
(2)令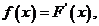 若
若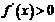 的解集为A,且
的解集为A,且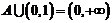 ,求
,求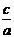 的范围
的范围
解:(I)∵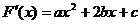 ,且
,且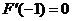 ,
,
∴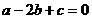 ①④
①④
又由在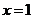 处取得极小值-2可知
处取得极小值-2可知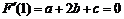 ②且
②且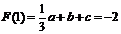 ③
③
将①②③式联立得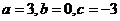 ∴
∴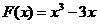 。
。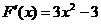 (4分)
(4分)
由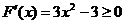 得
得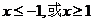 同理由
同理由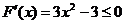 得
得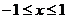
∴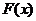 的单调递减区间是[-1,1], 单调递增区间是(-∞,1
的单调递减区间是[-1,1], 单调递增区间是(-∞,1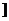 和
和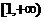 (6分)
(6分)
(II)由上问知: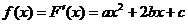 ,∴
,∴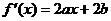 。
。
又∵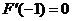 。∴
。∴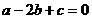 。∴
。∴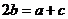 。∴
。∴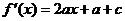
∵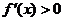 ,∴
,∴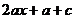 >0。∴
>0。∴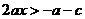 。(8分)
。(8分)
∴当 时,
时,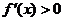 的解集是
的解集是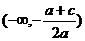 ,
,
显然A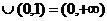 不成立,不满足题意。
不成立,不满足题意。
∴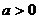 ,且
,且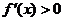 的解集是
的解集是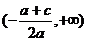 。 (10分)
。 (10分)
又由A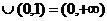 知
知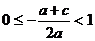 。解得
。解得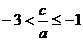 。(12分)
。(12分)
79、(山西省实验中学2007-2008学年度高三年级第四次月考)设函数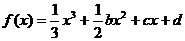 (b、c、d为常数),方程
(b、c、d为常数),方程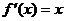 有两个实数x1、x2,且
有两个实数x1、x2,且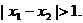
(1)求证: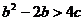
(2)若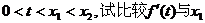 的大小
的大小
(3)若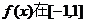 上的切线倾斜角取值范围是
上的切线倾斜角取值范围是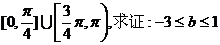
解:(1)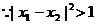
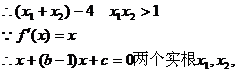
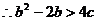 …………4分
…………4分
(2)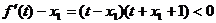
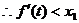 …………8分
…………8分
(3)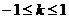

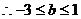 …………12分
…………12分
78、(山东省实验中学2008届高三第三次诊断性测试)已知函数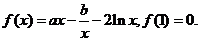
(1)若函数 在其定义域内为单调函数,求实数
在其定义域内为单调函数,求实数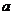 的取值范围;
的取值范围;
(2)若函数 的图象在
的图象在 处的切线的斜率为0,且
处的切线的斜率为0,且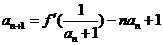 ,若
,若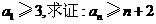 .
.
解:(1)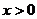
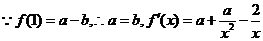
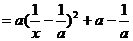 ,(2分)
,(2分)
①当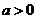 时,则有
时,则有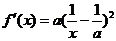
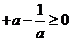 恒成立。即
恒成立。即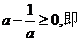
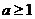
②当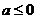 时,由x>0,知
时,由x>0,知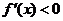 恒成立;
恒成立;
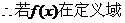 内为单调函数,
内为单调函数,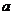 的取值范围为
的取值范围为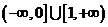 ..….….5分
..….….5分
(2)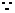 函数
函数 的图象在
的图象在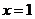 处的切线为斜率为0,
处的切线为斜率为0,
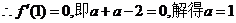 ,
,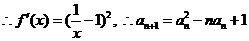 ………8分
………8分
用数学归纳法证明:(Ⅰ)当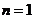 时,
时,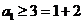 ,不等式成立;
,不等式成立;
(Ⅱ)假设当时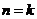 时,不等式成立,即
时,不等式成立,即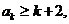 那么,
那么,
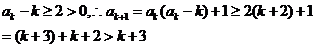
也就是说,当 时,
时,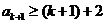 ,根据(Ⅰ)(Ⅱ)对于所有
,根据(Ⅰ)(Ⅱ)对于所有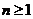 有
有
 ………………………….12分
………………………….12分
77、(山东省济南市2008年2月高三统考)已知定义在正实数集上的函数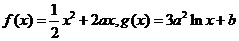 ,其中
,其中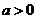 。设两曲线
。设两曲线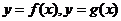 有公共点,且在公共点处的切线相同。
有公共点,且在公共点处的切线相同。
(1)若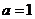 ,求
,求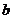 的值;
的值;
(2)用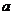 表示
表示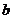 ,并求
,并求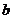 的最大值。
的最大值。
解:(1)设 与
与 在公共点
在公共点 处的切线相同
处的切线相同
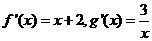 1分
1分
由题意知 ,∴
,∴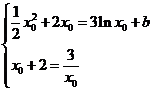
由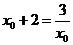 得,
得,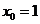 ,或
,或 (舍去) 4分
(舍去) 4分
即有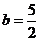 5分
5分
(2)设 与
与 在公共点
在公共点 处的切线相同
处的切线相同
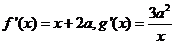
由题意知 ,∴
,∴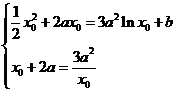
由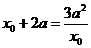 得,
得, ,或
,或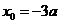 (舍去) 7分
(舍去) 7分
即有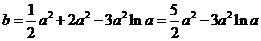 8分
8分
令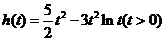 ,则
,则 ,于是
,于是
当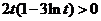 ,即
,即 时,
时,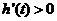 ;
;
当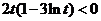 ,即
,即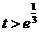 时,
时,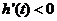 10分
10分
故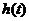 在
在 的最大值为
的最大值为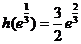 ,故
,故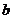 的最大值为
的最大值为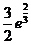 12分
12分
76、(宁夏区银川一中2008届第六次月考)已知函数f(x)=ex–kx,x R
R
(1)若k=e,试确定函数f(x)的单调区间。
(2)若k>0,且对于任意x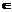 R,f(|x|)>0恒成立,试确定实数k的取值范围
R,f(|x|)>0恒成立,试确定实数k的取值范围
(3)设函数F(x)=f(x)+f(-x),求证:
F(1)F(2)…F(n)=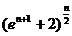
解:(1)由K=e得f(x)=ex-ex, 所以f’(x)=ex-e. 由f’(x)>0得x>1,故f(x)的单调增区间
为(1,+∞),由f’(x)<0得x<1,故f(x)的单调递减区间为(-∞,1)(3分)
(2)由f(|x|)>0对任意x∈R成立等价于f(x)>0对任意x≥0成立。由f’(x)=ex-k=0得x=lnk.
①当k∈(0,1) 时 ,f’(x)=ex-k ≥1-k≥0(x>0),此时f(x)在(0,+∞上单调递增,
故f(x)≥f(0)=1>),符合题意。②当k∈(1,+∞)时,lnk>0,当X变化时,f’(x)、f(x)的变化情况
如下表:
|
X |
(0,lnk) |
lnk |
(lnk,+ ∞) |
|
f’(x) |
- |
0 |
+ |
|
f(x) |
单调递减 |
极小值 |
单调递增 |

由此可得,在(0,+∞)上f(x)≥f(lnk)=k-lnk.依题意,k-klnk>0,又k>1,所以1<k<e.综上所述,实数k的取值范围是0<k<e. (8分)
(3)因为F(x)=f(x)+f(-x)=ex+e-x,所以F(x1)F(x2)=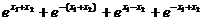
≥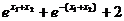 ≥
≥ 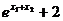 ,
,
所以F(1)F(n)>en+1+2,F(2)F(n-1)>en+1+2
……F(n)F(1)>en+1+2.
由此得,[F(1)F(2)…F(n)]2=[F(1)F(n)][F(2)F(n-1)]…[F(n)F(1)]>(en+1+2)n
故F(1)F(2)…F(n)>(en+1+2)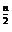 ,n∈N* (12分)
,n∈N* (12分)
75、(江西省鹰潭市2008届高三第一次模拟)设函数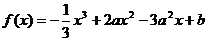 ,
,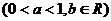
(1)求函数 的单调区间和极值
的单调区间和极值
(2)若当 时,恒有
时,恒有 ,试确定
,试确定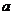 的取值范围
的取值范围
解:(1) f(x)的导函数f ¢(x)=-x2+4ax-3a2 =-(x-2a)2+a2 ……………2分
∵f ¢(x)在区间(0,1)上存在反函数
∴ 2a≤0或2a≥1 …………………4分
又∵0<a<1
∴a的取值范围是 ≤a<1 …………………6分
(2)由| f ¢(x) | ≤a,得 -a≤-x2+4ax-3a2≤a
∵a+1>2a,∴f ¢(x)在[ a+1 , a+2 ]上是减函数。…………………8分
∴f ¢(x)max = f ¢(a+1)=2a-1………………………9分
f ¢(x)min = f ¢(a+2)=4a-4………………10分
∴解得 ≤a<1 ………………12分
74、(江苏省盐城市2008届高三六校联考)已知函数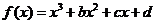 (b,c,d∈R且都为常数)的导函数
(b,c,d∈R且都为常数)的导函数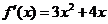 且f(1)=7,设
且f(1)=7,设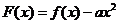
(1)当a<2时,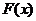 的极小值;
的极小值;
(2)若对任意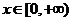 都有
都有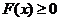 成立,求a的取值范围;
成立,求a的取值范围;
(3)在(2)的条件下比较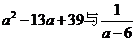 的大小.
的大小.
(1)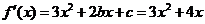
∴2b=4 c=0 ∴b=2 c=0
∴
f(1)=7 d=4 ∴f(x)=x3+2x2+4 ……………………………………2分
∵F(x)=f(x)-ax2=x3+(2-a)x2+4
则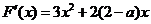
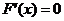 x1=0 x2=-
x1=0 x2=-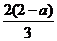
∵a<2 ∴x1>x2
故由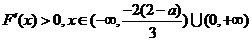
∴F(x)在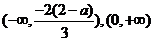 上单调增在
上单调增在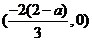 上单调减
上单调减
故x=0时F(x)取得极小值为F(0)=4 ………………………………………………5分
(2)F(x)≥0恒成立 当x∈[0,+∞)时F(x)最小值≥0
①当2-a>0即a<2时由(1)知F(x)min=F(0)=4>0符合题意 ………………………7分
②若2-a≤0,即a≥2时,由(1)知x1<x2
∴当x∈[0,+∞)时,F(x)min=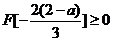
即
a≤5 ∴2≤a≤5
综上所述 a≤5 ……………………………………………………………………10分
(3)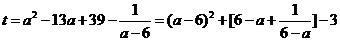 ……………………12分
……………………12分
∵a≤5 ∴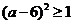 6-a≥1
6-a≥1
故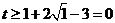
∴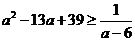 (等号在a=5时成立) …………………………………14分
(等号在a=5时成立) …………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com