
1.教学重点:指数形式的函数图象、性质的应用.
3.情感、态度与价值观
(1) 认识从特殊到一般的研究方法.
(2) 了解数学在生产实际中的应用.
2.过程与方法:
(1)让学生了解数学来自生活,数学又服务于生活的哲理;
(2)培养学生观察问题,分析问题的能力.
1.知识与技能:
(1)熟练掌握指数函数概念、图象、性质;
(2)掌握指数形式的函数定义域、值域的求法,以及单调性、奇偶性判断;
(3)培养学生数学应用意识
教学 环节 |
教学内容 |
师生互动 |
设计意图 |
||||||||||||||||||||||||||||||||||||||||||||
复习 引入 |
1. 在本章的开头,问题(1)中时间 与GDP值中的 与GDP值中的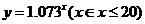   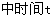    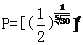 , , 请问这两个函数有什么共同特征.  2. 这两个函数有什么共同特征  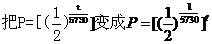 ,从而得出这两个关系式中的底数是一个正数,自变量为指数,即都可以用 ,从而得出这两个关系式中的底数是一个正数,自变量为指数,即都可以用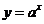 ( (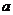 >0且 >0且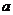 ≠1来表示). ≠1来表示). |
学生思考回答函数的特征. |
由实际问题引入,不仅能激发学生的学习兴趣,而且可以培养学生解决实际问题的能力. |
||||||||||||||||||||||||||||||||||||||||||||
形成概念        理解概念  |
指数函数的定义 一般地,函数 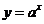 ( (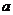 >0且 >0且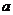 ≠1)叫做指数函数,其中 ≠1)叫做指数函数,其中 是自变量,函数的定义域为R. 是自变量,函数的定义域为R. 回答:在下列的关系式中,哪些不是指数函数,为什么?  (1) 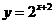  (2) 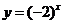  (3) 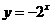  (4) 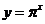  (5) 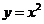
 (6) 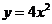  (7) 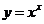  (8) 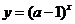 ( (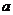 >1,且 >1,且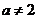 ) ) 小结:根据指数函数的定义来判断说明:因为 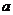 >0, >0, 是任意一个实数时, 是任意一个实数时,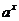 是一个确定的实数,所以函数的定义域为实数集R. 是一个确定的实数,所以函数的定义域为实数集R. 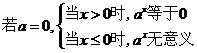  若 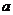 <0, <0, 如 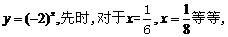 在实数范围内的函数值不存在. 在实数范围内的函数值不存在. 若 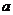 =1, =1, 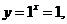 是一个常量,没有研究的意义,只有满足 是一个常量,没有研究的意义,只有满足 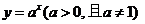 的形式才能称为指数函数, 的形式才能称为指数函数,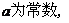  如: 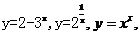  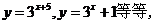 不符合 不符合 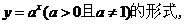 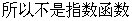 . . |
学生独立思考,交流讨论,教师巡视,并注意个别指导, 学生探讨分析,教师点拨指导. |
由特殊到一般,培养学生的观察、归纳、概括的能力.  使学生进一步理解指数函数的概念. |
||||||||||||||||||||||||||||||||||||||||||||
|
深化 概念 |
我们在学习函数的单调性的时候,主要是根据函数的图象,即用数形结合的方法来研究. 下面我们通过 先来研究 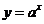 ( (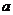 >1)的图象, >1)的图象,用计算机完成以下表格,并且用计算机画出函数 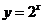 的图象 的图象
再研究先来研究 用计算机完成以下表格并绘出函数
从图中我们看出
通过图象看出
讨论:
问题:从画出的图象中,你能发现函数的图象与底数间有什么样的规律. 从图上看 |
学生列表计算,描点、作图. 教师动画演示. 学生观察、归纳、总结,教师诱导、点评. |
通过列表、计算使学生体会、感受指数函数图象的化趋势,通过描点,作图培养学生的动手实践能力. 不同情况进行对照,使学生再次经历从特殊到一般,由具体到抽象的思维过程.培养学生的归纳概括能力. |
||||||||||||||||||||||||||||||||||||||||||||
|
应用 举例 |
例1:(P66 例6)已知指数函数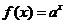 ( (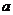 >0且 >0且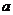 ≠1)的图象过点(3,π),求 ≠1)的图象过点(3,π),求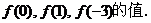 |
学生思考、解答、交流,教师巡视,注意个别指导,发现带有普遍性的问题,应及时提到全体学生面前供大家讨论. 例1分析:要求 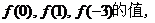  再把0,1,3分别代入 再把0,1,3分别代入 ,即可求得 ,即可求得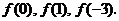 解:将点(3,π),代入 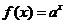 得到 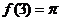 , ,即 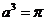 , ,解得: 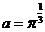 ,于是 ,于是 , ,所以 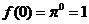 , ,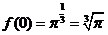 , , . . |
巩固所学知识,培养学生的数形结合思想和创新能力. |
||||||||||||||||||||||||||||||||||||||||||||
|
归纳 总结 |
1、理解指数函数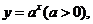 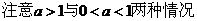 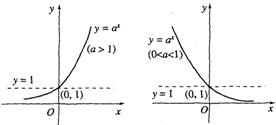 2、解题利用指数函数的图象,可有利于清晰地分析题目,培养数型结合与分类讨论的数学思想 . |
学生先自回顾反思,教师点评完善. |
通过师生的合作总结,使学生对本节课所学知识的结构有一个明晰的认识,形成知识体系. |
||||||||||||||||||||||||||||||||||||||||||||
|
课后 作业 |
作业:2.1 第四课时 习案 |
学生独立完成 |
巩固新知 提升能力 |
备选例题
例1 指出下列函数哪些是指数函数:
(1)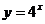 ; (2)
; (2)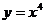 ;
;
(3)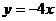 ;
(4)
;
(4)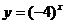 ;
;
(5)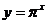 ; (6)
; (6)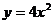 ;
;
(7)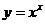 ; (8)
; (8)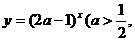 且
且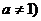 .
.
[分析] 根据指数函数定义进行判断.
[解析] (1)、(5)、(8)为指数函数;
(2)是幂函数(后面2.3节中将会学习);
(3)是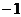 与指数函数
与指数函数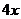 的乘积;
的乘积;
(4)底数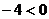 ,
,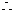 不是指数函数;
不是指数函数;
(6)指数不是自变量 ,而底数是
,而底数是 的函数;
的函数;
(7)底数 不是常数.
不是常数.
它们都不符合指数函数的定义.
[小结]准确理解指数函数的定义是解好本问题的关键.
例2 用计算机作出的图像,并在同一坐标系下作出下列函数的图象,并指出它们与指数函数y=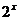 的图象的关系,
的图象的关系,
⑴y=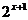 与y=
与y=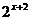 .
.
⑵y=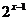 与y=
与y=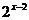 .
.
解:⑴作出图像,显示出函数数据表
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
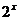 |
0.125 |
0.25 |
0.5 |
1 |
2 |
4 |
8 |
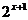 |
0.25 |
0.5 |
1 |
2 |
4 |
8 |
16 |
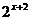 |
0.5 |
1 |
2 |
4 |
8 |
16 |
32 |
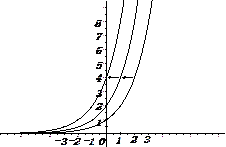
比较函数y=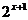 、y=
、y=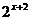 与y=
与y=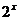 的关系:将指数函数y=
的关系:将指数函数y=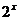 的图象向左平行移动1个单位长度,就得到函数y=
的图象向左平行移动1个单位长度,就得到函数y=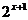 的图象,将指数函数y=
的图象,将指数函数y=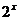 的图象向左平行移动2个单位长度,就得到函数y=
的图象向左平行移动2个单位长度,就得到函数y=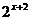 的图象
的图象
⑵作出图像,显示出函数数据表
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
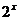 |
0.125 |
0.25 |
0.5 |
1 |
2 |
4 |
8 |
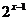 |
0.625 |
0.125 |
0.25 |
0.5 |
1 |
2 |
4 |
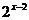 |
0.3125 |
0.625 |
0.125 |
0.25 |
0.5 |
1 |
2 |
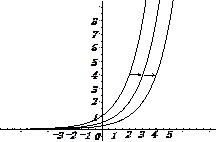
比较函数y=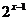 、y=
、y=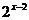 与y=
与y=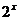 的关系:将指数函数y=
的关系:将指数函数y=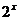 的图象向右平行移动1个单位长度,就得到函数y=
的图象向右平行移动1个单位长度,就得到函数y=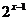 的图象,将指数函数y=
的图象,将指数函数y=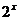 的图象向右平行移动2个单位长度,就得到函数y=
的图象向右平行移动2个单位长度,就得到函数y=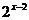 的图象
的图象
小结:⑴当m>0时,将指数函数y=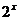 的图象向右平行移动m个单位长度,就得到函数y=
的图象向右平行移动m个单位长度,就得到函数y=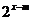 的图象;当m>0时,将指数函数y=
的图象;当m>0时,将指数函数y=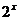 的图象向左平行移动m个单位长度,就得到函数y=
的图象向左平行移动m个单位长度,就得到函数y=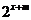 的图象
的图象
采用观察、分析、归纳、抽象、概括,自主探究,合作交流的教学方法,通过各种教学媒体(如计算机或计算器),调动学生参与课堂教学的主动性和积极性.
2.教学难点:指数函数的概念和图象.
1.教学重点:指数函数的概念和图象.
3.情感、态度与价值观
在解决简单实际问题的过程中,体会指数函数是一类重要的函数模型,激发学生学习数学的兴趣,努力培养学生的创新意识.
2.过程与方法
能借助计算器或计算机画出具体指数函数的图象,探索指数函数图象特征.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com