
21.设函数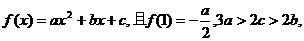
求证:(1)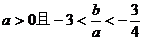 ;
;
(2)函数 在区间(0,2)内至少有一个零点;
在区间(0,2)内至少有一个零点;
(3)设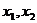 是函数
是函数 的两个零点,则
的两个零点,则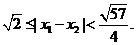
证明:(1)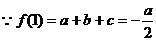
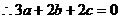
又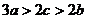
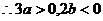
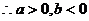 ……………………2分
……………………2分
又2c=-3a-2b 由3a>2c>2b ∴3a>-3a-2b>2b
∵a>0 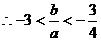 ………………………………………………4分
………………………………………………4分
(2)∵f(0)=c,f(2)=4a+2b+c=a-c………………………………6分
①当c>0时,∵a>0,∴f(0)=c>0且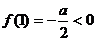
∴函数f(x)在区间(0,1)内至少有一个零点……………………8分
②当c≤0时,∵a>0 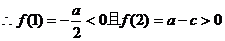
∴函数f(x)在区间(1,2)内至少有一个零点.
综合①②得f(x)在(0,2)内至少有一个零点…………………………10分
(3)∵x1,x2是函数f(x)的两个零点
则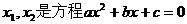 的两根
的两根
∴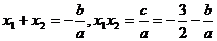 ……………………………………12分
……………………………………12分
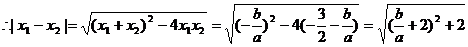
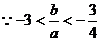
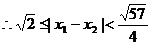 ………………………………14分
………………………………14分
20.已知函数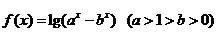
(1)求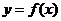 的定义域;
的定义域;
(2)在函数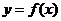 的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
(3)当a、b满足什么条件时, 在
在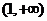 上恒取正值。
上恒取正值。
解(1)由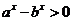 得
得 ,且
,且 ,得
,得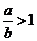 ,所以
,所以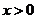 ,即
,即 的定义域为
的定义域为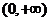 。
。
(2)任取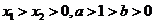 ,则
,则 ,所以
,所以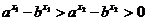 ,即
,即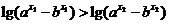 ,故
,故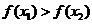 。所以
。所以 在
在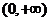 为增函数;假设函数
为增函数;假设函数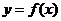 的图象上存在不同的两点
的图象上存在不同的两点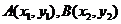 ,使直线平行于x轴,则
,使直线平行于x轴,则 。这与
。这与 是增函数矛盾。故函数
是增函数矛盾。故函数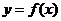 的图象上不存在不同的两点使过两点的直线平行于x轴。
的图象上不存在不同的两点使过两点的直线平行于x轴。
(3)因为 是增函数,所以当
是增函数,所以当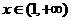 时,
时,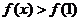 。这样只需
。这样只需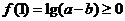 ,即当
,即当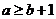 时,
时, 在
在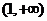 上恒取正值。
上恒取正值。
19. 设函数
设函数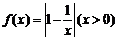 。
。
(1)求 的单调区间;
的单调区间;
(2)是否存在正实数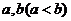 ,使函数
,使函数 的定义域为
的定义域为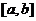 时值域为
时值域为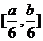 ?
?
若存在,求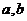 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
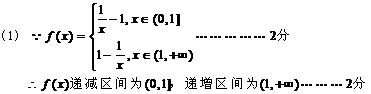
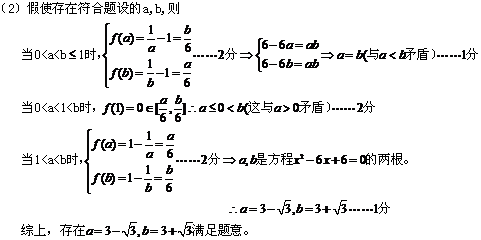
18.已知函数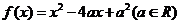
(1)如果关于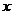 的不等式
的不等式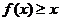 的解集为
的解集为 ,求实数
,求实数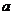 的最大值;
的最大值;
(2)在(1)的条件下,对于任意实数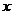 ,试比较
,试比较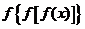 与
与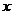 的大小;
的大小;
(3)设函数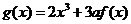 ,如果
,如果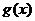 在区间
在区间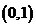 上存在极小值,求实数
上存在极小值,求实数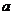 的取值范围。
的取值范围。
解(1)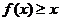 的解集为
的解集为 ,
,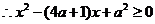 恒成立
恒成立
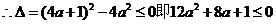 解得
解得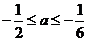 ,
,
故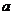 的最大值为
的最大值为
(2)由(1)得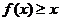 恒成立,
恒成立,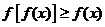 ,
,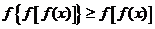
从而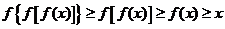 ,即
,即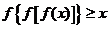
(3)由已知可得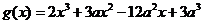 ,则
,则
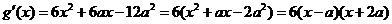
令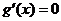 得
得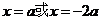
① 若 ,则
,则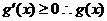 在
在 上单调递增,在
上单调递增,在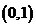 上无极值
上无极值
② 若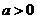 ,则当
,则当 时,
时,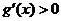 ;当
;当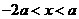 时,
时,
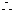 当
当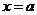 时,
时,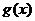 有极小值
有极小值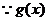 在区间
在区间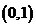 上存在极小值,
上存在极小值,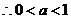
③ 若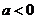 ,则当
,则当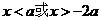 时,
时,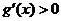 ;当
;当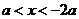 时,
时,
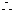 当
当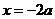 时,
时,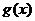 有极小值
有极小值 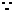
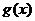 在区间
在区间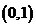 上存在极小值
上存在极小值
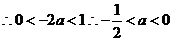
综上所述:当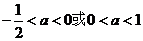 时,
时,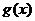 在区间
在区间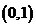 上存在极小值
上存在极小值
17.已知函数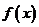 =
=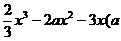 ∈R).
∈R).
(1)当|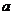 |≤
|≤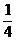 时,求证:
时,求证: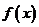 在(-1,1)内是减函数;
(2)若函数
在(-1,1)内是减函数;
(2)若函数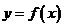 在区间(-1,1)内有且只有一个极值点,求
在区间(-1,1)内有且只有一个极值点,求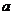 的取值范围.
的取值范围.
16.平面区域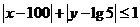 的面积为
.
的面积为
.
解:平面区域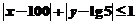 是通过平面区域 |x|+|y |
是通过平面区域 |x|+|y |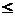 1平移而得到的,而平面区域 |x|+|y |
1平移而得到的,而平面区域 |x|+|y |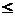 1的面积即为曲线|x|+|y |=1所围成区域的面积,其值为2,故所求面积为2.
1的面积即为曲线|x|+|y |=1所围成区域的面积,其值为2,故所求面积为2.
15.已知1+2x+3x·a≥0在(-∞,1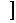 上恒成立,则a的取值范围为
.(a≥-1)
上恒成立,则a的取值范围为
.(a≥-1)
解:∵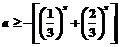 ,
且函数
,
且函数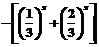 为增函数,
为增函数,
∴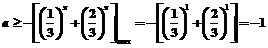 .
.
14.若定义在R上的函数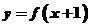 的反函数是
的反函数是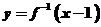 ,且
,且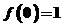 ,则
,则 .(2007)
.(2007)
解:∵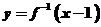 的反函数为
的反函数为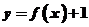 ,∴
,∴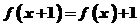 ,∴
,∴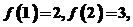 …
… .
.
13.函数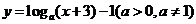 的图象恒过定点
的图象恒过定点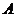 ,若点
,若点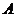 在直线
在直线 上,其中
上,其中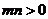 ,则
,则 的最小值为_______8
的最小值为_______8
12.已知函数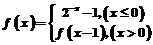 若方程
若方程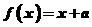 有且只有两个不相等的实根,则实数a的取值范围是( C ).A.
有且只有两个不相等的实根,则实数a的取值范围是( C ).A. 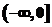 B.
B.
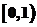 C.
C.
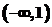 D.
D.
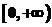
解:据题意,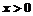 时,
时,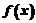 是周期为1的周期函数,且当
是周期为1的周期函数,且当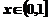 时
时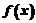 的函数值为
的函数值为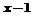 所得到的
所得到的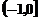 时的函数值,即
时的函数值,即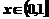 的图像是
的图像是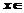
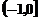 的图像向右平移一个单位得到的. 又∵
的图像向右平移一个单位得到的. 又∵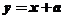 与
与 的图像恰有两个交点,∴
的图像恰有两个交点,∴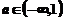 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com