
6.子集:若集合A中 都是集合B的元素,就说集合A包含于集合B(或集合B包含集合A),记作 .
5.集合与集合的关系用符号 表示.
4.元素与集合是属于和 的从属关系,若a是集合A的元素,记作 ,若a不是集合B的元素,记作 .但是要注意元素与集合是相对而言的.
3.集合的表示法常用的有 、 和韦恩图法三种,有限集常用 ,无限集常用 ,图示法常用于表示集合之间的相互关系.
2.集合中的元素属性具有:
(1) 确定性; (2) ; (3) .
1.集合是一个不能定义的原始概念,描述性定义为:某些指定的对象 就成为一个集合,简称 .集合中的每一个对象叫做这个集合的 .
10.2 10
分别计算上面两个样本的平均数与方差.如果图纸上的设计尺寸为10mm,从计算结果看,用哪台机床加工这种零件较合适.
解: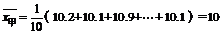

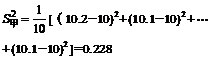
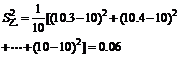
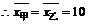 ,
,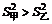
所以乙比甲稳定,用乙较合适.
变式训练2:假定下述数据是甲乙两个供货商的交货天数:
甲:10 9 10 10 11 11 9 11 10 10
乙:8 10 14 7 10 11 10 8 15 12
估计两个供货商的交货情况,并问哪个供货商交货时间短一些,哪个供货商交货时间较具一致性与可靠性.
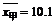

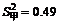

从交货天数的平均值看来,甲供货商的供货天数短一些;从方差来看,甲供货商的交货天数较稳定,因此是较具一致性与可靠性的供货商.
例3. 个体户王某经营一家餐馆,下面是餐馆所有工作人员在某个月份的工资:
|
王某 |
厨师甲 |
厨师乙 |
杂工 |
招待甲 |
招待乙 |
会计 |
|
3000元 |
450元 |
400元 |
320元 |
350元 |
320元 |
410元 |
(1)计算平均工资;
(2) 计算出的平均工资能否反映帮工人员这个月收入的一般水平?
(3)去掉王某工资后,再计算平均工资;
(4)后一个平均工资能代表帮工人员的收入吗?
(5)根据以上计算,从统计的观点看,你对(1)、(3)的结果有什么看法?
解:(1)平均工资750元;
(2)因为帮工人员的工资低于平均工资,所以(1)中算出的平均工资不能反映帮工人员在这个月份的月收入的一般水平;(3)去掉王某的工资后的平均工资375元;(4)(3)中计算的平均工资接近于帮工人员月工资收入,所以它能代表帮工人员的收入;(5)从本题的计算可见,个别特殊值对平均数具有很大的影响,因此在选择样本时,样本中尽量不要选特殊数据.
变式训练3:甲乙两人在相同条件下,射靶10次,命中环数如下:
甲:8 6 9 5 10 7 4 8 9 5
乙:7 6 5 8 6 9 6 8 7 7
依上述数据估计 ( )
A.甲比乙的射击技术稳定
B.乙比甲的射击技术稳定
C.两人没有区别
D.两人区别不大
解:B
例4. 为了科学地比较考试成绩,有些选拔性考试常常会将考试分数转化为标准分,转化关系式为:z=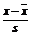 (其中x是某位同学的考试分数,
(其中x是某位同学的考试分数,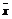 是该次考试的平均分,s是该次考试的标准差,z称为这位学生的标准分).转化为标准分后可能出现小数和负值,因此,又常常将z分数作线性变换转化或其他分数,例如某次学生选拔考试采用的是T分数,试性变换公式是:T=40z+60,已知在这次考试中某位考生的考试分数是85,这次考试的平均分是70,标准差是25,则该考生的T分数为多少?
是该次考试的平均分,s是该次考试的标准差,z称为这位学生的标准分).转化为标准分后可能出现小数和负值,因此,又常常将z分数作线性变换转化或其他分数,例如某次学生选拔考试采用的是T分数,试性变换公式是:T=40z+60,已知在这次考试中某位考生的考试分数是85,这次考试的平均分是70,标准差是25,则该考生的T分数为多少?
解:84分
变式训练4:经问卷调查,某班学生对摄影分别执“喜欢”,“不喜欢”和“一般”三种态度,其中执“一般”态度的比“不喜欢“的多12人,按分层抽样方法从全班选出部分学生座谈摄影,如果选出的是:5位“喜欢”摄影的同学,1位“不喜欢”摄影的同学和3位执“一般”态度的同学,那么全班学生中“喜欢”摄影的人数为多少?
解:设班里“喜欢”的y人,“一般”的x人,“不喜欢”的x-12人.
∴ ∴x=18
∴x=18
又 ∴y=30
∴y=30
即全班“喜欢”摄影的人数为30.
|
方差是反映稳定性程度的一个重要特征,在日常生活中常有体现,如两同学的总成绩都一样,但是一个人有偏科现象,而另一个人没有,一般认为没有偏科现象(即方差小)的同学成绩要稳定一些.
9.9 10.1
乙: 10.3 10.4 9.6 9.9 10.1 10 9.8 9.7
3.方差(1)
 分别称为数据
分别称为数据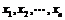 的方差和标准差,它们反映的是数据的稳定与波动,集中与离散的程度.
的方差和标准差,它们反映的是数据的稳定与波动,集中与离散的程度.
(2)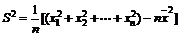
(3)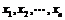 数值较大时,可以将各数据减去一个恰当的常数a,得到
数值较大时,可以将各数据减去一个恰当的常数a,得到
|
 则
则
例1.某班40人随机平均分成两组,两组学生一次考试的成绩情况如下表:
|
统计量 级别 |
平均 |
标准差 |
|
第一组 |
90 |
6 |
|
第二组 |
80 |
4 |
求全班的平均成绩和标准差.
解:设第一组20名学生的成绩为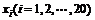 ;
;
第二组20名学生的成绩为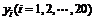 ,
,

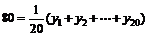 故全班平均成绩为:
故全班平均成绩为:
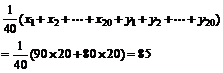
又设第一组学生的成绩的标准差为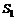 ,第二组学生的成绩的标准差为
,第二组学生的成绩的标准差为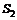 ,则
,则


此处(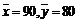 )
)
又设全班40名学生的标准差为S,平均成绩为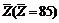 故有
故有
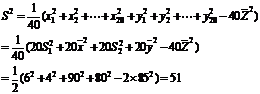
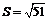
变式训练1:对甲乙的学习成绩进行抽样分析,各抽5门功课,得到的观测值如下:
甲:60 80 70 90 70
乙:80 60 70 80 75
问:甲乙谁的各科平均成绩好?谁的各门功课发展较平衡?
解: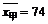
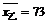

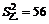 因为
因为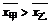 ,
,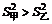 .所以甲的平均成绩较好,乙的各门发展较平衡.
.所以甲的平均成绩较好,乙的各门发展较平衡.
例2. 甲乙两台机床在相同的条件下同时生产一种零件,现在从中各抽测10个,它们的尺寸分别为(单位:mm)
甲: 10.2 10.1 10.9 8.9 9.9 10.3 9.7 10
2.样本平均数(也称样本期望值)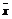
(1)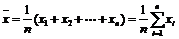 反映的是这组数据的平均水平.
反映的是这组数据的平均水平.
(2)当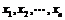 数值较大时,可将各个数据同时减去一个适当的数
数值较大时,可将各个数据同时减去一个适当的数 ,得
,得 =
=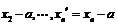 ,那么
,那么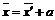
(3)如果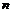 个数据中,
个数据中,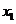 出现
出现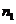 次,
次, 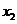 出现
出现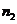 次,…,
次,…, 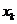 出现
出现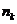 次,那么:
次,那么:

这里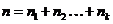
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com