
3.自然资源的综合利用
(1)工业上从海水中提取溴的过程如下:
2Br-+Cl2=Br2+2Cl-,Br2+3Na2CO3= 5NaBr+NaBrO3+2CO2
5NaBr+NaBrO3+3H2SO4=3Na2SO4+3Br2+3H2O
(2)以海水为原料制备金属镁:
MgCl2+Ca(OH)2=Mg(OH)2+CaCl2,
Mg(OH)2+2HCl=MgCl2+2H2O,MgCl2 Mg+Cl2↑
Mg+Cl2↑
(3)从铝土矿中提炼金属铝:2Al2O3 4Al+3O2↑
4Al+3O2↑
(4)工业制氯气及烧碱:原理:2NaCl+2H2O 2NaOH+Cl2↑+H2↑原料:纯净的饱和食盐水;设备:离子交换膜电解槽;其他:食盐水的精制;离子交换膜的作用及特点。
2NaOH+Cl2↑+H2↑原料:纯净的饱和食盐水;设备:离子交换膜电解槽;其他:食盐水的精制;离子交换膜的作用及特点。
(5)硫酸的工业制法
4FeS2+11O2 2Fe2O3+8SO2(沸腾炉内进行)
2Fe2O3+8SO2(沸腾炉内进行)
2SO2+O2 2SO3(接触室中进行)
2SO3(接触室中进行)
SO3+H2O=H2SO4(在吸收塔内用98.3%的浓H2SO4吸收)
(6)硝酸的工业制法:
氨催化氧化成NO(氧化炉):
4NH3+5O2  4NO+6H2O
4NO+6H2O
HNO3的生成(吸收塔)2NO+O2===2NO2,3NO2+H2O===2HNO3+NO↑(放出的NO被氧化再被吸收)得到50%的HNO3,经Mg(NO3)2或浓H2SO4处理再蒸馏浓缩,可得96%以上的浓HNO3。
(7)玻璃工业
Na2CO3+SiO2 Na2SiO3+CO2↑
Na2SiO3+CO2↑
CaCO3+SiO2 CaSiO3+CO2↑
CaSiO3+CO2↑
[典型例析]
例1:下列有关环境问题的说法正确的是
A.燃煤时加入适量石灰石,可减少废气中SO2的量
B.臭氧的体积分数超过10-4%的空气有利于人体健康
C.pH在5.6~7.0之间的降水通常称为酸雨
D.含磷合成洗涤剂易于被细菌分解,故不会导致水体污染
变式训练:
六价铬对人体有毒,含铬废水要经过化学处理后才能排放。方法是用绿矾(FeSO4·7H2O)把废水中的六价铬还原成三价铬离子,再加入过量石灰水后,使铬离子转化为氢氧化铬(Cr(OH)3)沉淀,其主要反应的化学方程式如下:H2Cr2O7+6FeSO4+6H2SO4==3Fe2(SO4)3+Cr2(SO4)3+7H2O。现用上法处理1×104 L含铬(+6价)78 mg·L-1的废水(Cr的相对原子质量为52),试回答:
(1)处理后沉淀除Cr(OH)3外,还有__(用化学式来表示)。
(2)需要用绿矾多少千克?
例2:已知某一硅酸盐可表示为Mga(Si4O10)(OH)b(其中a、b为正整数)。试问:
(1)a与b应满足的关系____________(填写表达式);
(2)a能否等于2?________(填“能”“不能”“无法确定”);
(3)分别写出a=4和b=6时硅酸盐的表达式_______(以氧化物的形式表示)。
变式训练:
下列有关新型高分子材料的说法不正确的是
A.高分子分离膜应用于食品工业中,可用于浓缩天然果汁、乳制品加工、酿造业等
B.复合材料一般是以一种材料作为基体,另一种材料作为增强剂
C.导电塑料是应用于电子工业的一种新型有机高分子材料
D.合成高分子材料制成的人工器官都受到人体的排斥作用,难以达到生理相容的程度
例3:下图是从铝土矿X中提取其主要成分的两种相互结合的方案,已知A为红褐色沉淀,D、F为白色沉淀,F经两次失水转化为G,Ⅰ、Ⅱ、Ⅲ、Ⅳ是相同的操作。

(1)操作Ⅰ的名称是__________,
(2)X的主要成分是________、_______、 (用氧化物的化学式表示)。
(3)写出下列转化的离子方程式:
B+C→D___________________________;
N→F ___________________________。
(4)要使X的利用率最高,则方案一与方案二所取矿石的质量比为__________。
(5)两方案结合的优点是 。
变式训练:
工业上从海水中提取溴采用下列方法:(1)向海水中通入Cl2,将海水中的溴化物氧化,其离子方程式为: 。
(2)向上述混合液中吹入热空气,将生成的溴吹出并用纯碱溶液吸收使其生成NaBr、NaBrO3,其化学方程式为 。(3)将(2)所得溶液用H2SO4酸化,使NaBr、NaBrO3中的溴转化为单质溴,再用有机溶剂提取溴后还可得到副产品Na2SO4,写出这一过程的化学方程式 。(4)这样得到的溴中还混有少量Cl2,怎样除去?
[当堂反馈]
2.材料
(1)新型无机材料:新型无机材料按其在使用中的作用和要求可分为结构材料和功能材料。结构材料主要是应用于具有耐高温、耐化学腐蚀的坚固耐用材料;功能材料是利用其所具有的特殊的力学、热学、光学、磁学及化学性质来完成特定功能的材料。如新型超导材料、纳米材料等。
(2)新型有机材料:新型有机材料是近年来大量合成的一类新型化学材料。它具有密度较小,强度较高,弹性、可塑性、绝缘性和耐腐蚀性好等优点。新型有机材料主要有塑料、合成纤维和合成橡胶等。合成新型有机材料的方法通常有加聚反应和缩聚反应。通过加聚反应合成的其单体一般含有不饱和碳原子(含C==C等)。通过缩聚反应合成的其单体一般含有-OH、-COOH、-NH2等官能团,且在合成过程中会脱去小分子物质(H2O、HCl等)。
(3)建议在复习过程中关注以下话题:金属;非金属;合金;半导体;超导材料;光导纤维;人造宝石;玻璃;水泥;纳米材料;航天材料;化学纤维;化学塑料;可降解塑料;陶瓷;高温结构陶瓷;半导体陶瓷;高分子导电材料;光功能高分子材料;橡胶;导电橡胶;环境材料;有机玻璃;玻璃钢;碳纤维;建筑材料;耐火材料;高强度材料;耐高温耐腐蚀材料;防弹玻璃;涂料;防水材料;建筑胶粘剂;复合材料;高吸水性树脂;离子交换树脂。
1.环境保护与环境污染
(1)环境污染:主要包括大气污染、水污染、土壤污染、食品污染等,还包括固体废弃物、放射性、噪声等污染。
(2)工业三废:废水、废气、废渣。
(3)常见的环境问题及它们对应的污染物。
|
环境问题 |
污染物 |
|
酸雨 |
SO2(主要)及NOx |
|
光化学烟雾 |
NOx及碳氢化合物 |
|
臭氧空洞 |
氟氯烃及NOx |
|
水体富营养化 |
含氮、磷的化合物 |
|
废旧电池污染 |
废旧电池中的汞、镉、铅等重金属离子 |
|
温室效应 |
主要是CO2,但CO2不算是大气污染物 |
|
白色污染 |
有机物如塑料等 |
①酸雨:pH小于5.6的降水称为酸雨。二氧化硫是导致酸雨的主要污染物:SO2+H2O H2SO3,2H2SO3+O2==2H2SO4(主要因素),
H2SO3,2H2SO3+O2==2H2SO4(主要因素),
2SO2+O2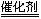 2SO3(催化剂指的是空气中的漂尘),SO3+H2O==H2SO4(次要因素)。
2SO3(催化剂指的是空气中的漂尘),SO3+H2O==H2SO4(次要因素)。
②臭氧层的破坏:一般氮氧化物和氯氟烃在破坏臭氧层的过程中起到催化剂的作用。
③温室效应:CO2、O3、CH4等气体能阻碍由地面反射回高空的红外辐射,这就像给地球罩上了一层保温膜,CO2等气体的过度排放,使地球表面的气温增加,产生温室效应。
(4)中学常见污染环境的气体及其防治
①SO2:工业上用浓氨水吸收,实验室用NaOH溶液吸收。②NOx:用NaOH溶液吸收,也可以用催化还原法。③H2S:用NaOH溶液吸收。④Cl2、Br2、HCl:实验室中常用NaOH溶液吸收,Cl2、Br2还可用Na2SO3吸收。工业上常用石灰乳吸收。⑤CO:用燃烧的方法除去。
3.对于给出集合是否为空集,集合中的元素个数是否确定,都是常见的讨论点,解题时要有分类讨论的意识.
2.集合的运算可以用韦恩图帮助思考,实数集合的交、并运算可在数轴上表示,注意在运算中运用数形结合思想.
1.在解决有关集合运算题目时,关键是准确理解题目中符号语言的含义,善于转化为文字语言.
4.A∪B=A
A∩B=A
|
例1. 设全集 ,
, 方程
方程 有实数根
有实数根 ,
, 方程
方程
有实数根 ,求
,求 .
.
解:当 时,
时, ,即
,即 ;
;
当 时,
时,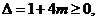 即
即 ,且
,且 ∴
∴ ,
,
∴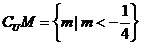
而对于 ,
, 即
即 ,∴
,∴ .
.
∴
变式训练1.已知集合A= B=
B=
(1)当m=3时,求 ;
;
(2)若A B
B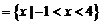 ,求实数m的值.
,求实数m的值.
解: 由 得
得 ∴-1<x≤5,∴A=
∴-1<x≤5,∴A= .
.
(1)当m=3时,B=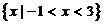 ,则
,则 =
= ,
,
∴ =
= .
.
(2)∵A= ∴有42-2×4-m=0,解得m=8.
∴有42-2×4-m=0,解得m=8.
此时B= ,符合题意,故实数m的值为8.
,符合题意,故实数m的值为8.
例2. 已知 ,
, 或
或 .
.
(1)若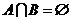 ,求
,求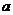 的取值范围;
的取值范围;
(2) 若 ,求
,求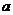 的取值范围.
的取值范围.
解:(1)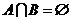 ,
∴
,
∴ ,解之得
,解之得 .
.
(2)  ,
∴
,
∴ . ∴
. ∴ 或
或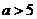 ,
,  或
或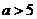
∴若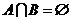 ,则
,则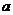 的取值范围是
的取值范围是 ;若
;若 ,则
,则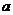 的取值范围是
的取值范围是 .
.
变式训练2:设集合A=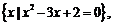 B
B
(1)若A B
B 求实数a的值;
求实数a的值;
(2)若A B=A,求实数a的取值范围;
B=A,求实数a的取值范围;
(3)若U=R,A (
(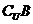 )=A.求实数a的取值范围.
)=A.求实数a的取值范围.
解:由x2-3x+2=0得x=1或x=2,故集合A=
(1)∵A B
B ∴2
∴2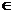 B,代入B中的方程,
B,代入B中的方程,
得a2+4a+3=0,∴a=-1或a=-3;
当a=-1时,B= 满足条件;
满足条件;
当a=-3时,B= 满足条件;
满足条件;
综上,a的值为-1或-3.
(2)对于集合B,
 =4(a+1)2-4(a2-5)=8(a+3).
=4(a+1)2-4(a2-5)=8(a+3).
∵A B=A,∴B
B=A,∴B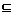 A,
A,
①当 <0,即a<-3时,B=
<0,即a<-3时,B= ,满足条件;
,满足条件;
②当 =0,即a=-3时,B
=0,即a=-3时,B ,满足条件;
,满足条件;
③当 >0,即a>-3时,B=A=
>0,即a>-3时,B=A= 才能满足条件,
才能满足条件,
则由根与系数的关系得
 即
即 矛盾;
矛盾;
综上,a的取值范围是a≤-3.
(3)∵A (
(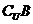 )=A,∴A
)=A,∴A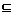
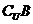 ,∴A
,∴A
①若B= ,则
,则 <0
<0 适合;
适合;
②若B≠ ,则a=-3时,B=
,则a=-3时,B= ,A
,A B=
B= ,不合题意;
,不合题意;
a>-3,此时需1 B且2
B且2 B,将2代入B的方程得a=-1或a=-3(舍去);
B,将2代入B的方程得a=-1或a=-3(舍去);
将1代入B的方程得a2+2a-2=0
∴a≠-1且a≠-3且a≠-1
综上,a的取值范围是a<-3或-3<a<-1- 或-1-
或-1- <a<-1或-1<a<-1+
<a<-1或-1<a<-1+ 或a>-1+
或a>-1+ .
.
例3. 已知集合A= B
B ,试问是否存在实数a,使得A
,试问是否存在实数a,使得A B
B 若存在,求出a的值;若不存在,请说明理由.
若存在,求出a的值;若不存在,请说明理由.
解:方法一
假设存在实数a满足条件A B=
B= 则有
则有
(1)当A≠ 时,由A
时,由A B=
B= ,B
,B ,知集合A中的元素为非正数,
,知集合A中的元素为非正数,
设方程x2+(2+a)x+1=0的两根为x1,x2,则由根与系数的关系,得

(2)当A= 时,则有
时,则有 =(2+a)2-4<0,解得-4<a<0.
=(2+a)2-4<0,解得-4<a<0.
综上(1)、(2),知存在满足条件A B=
B= 的实数a,其取值范围是(-4,+∞).
的实数a,其取值范围是(-4,+∞).
方法二 假设存在实数a满足条件A B≠
B≠ ,则方程x2+(2+a)x+1=0的两实数根x1,x2至少有一个为正,
,则方程x2+(2+a)x+1=0的两实数根x1,x2至少有一个为正,
因为x1·x2=1>0,所以两根x1,x2均为正数.
则由根与系数的关系,得 解得
解得
又∵集合 的补集为
的补集为
∴存在满足条件A B=
B= 的实数a,其取值范围是(-4,+∞).
的实数a,其取值范围是(-4,+∞).
变式训练3.设集合A={(x,y)|y=2x-1,x∈N*},B={(x,y)|y=ax2-ax+a,x∈N*},问是否存在非零整数a,使A∩B≠ ?若存在,请求出a的值;若不存在,说明理由.
?若存在,请求出a的值;若不存在,说明理由.
解:假设A∩B≠ ,则方程组
,则方程组
 有正整数解,消去y,得ax2-(a+2)x+a+1=0.
有正整数解,消去y,得ax2-(a+2)x+a+1=0.
由Δ≥0,有(a+2)2-4a(a+1)≥0,解得- .因a为非零整数,∴a=±1,
.因a为非零整数,∴a=±1,
当a=-1时,代入(*), 解得x=0或x=-1,
而x∈N*.故a≠-1.当a=1时,代入(*),
解得x=1或x=2,符合题意.故存在a=1,使得A∩B≠ ,
,
此时A∩B={(1,1),(2,3)}.
|
 ax+a2+a+2=0,x∈R},是否存在实数a,使得A
ax+a2+a+2=0,x∈R},是否存在实数a,使得A B=
B=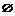 ?若存在,求出实数的值;若不存在,说明理由.
?若存在,求出实数的值;若不存在,说明理由.
解:1<a<2即实数 (1,2)时,
(1,2)时, =
=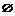 .
.
变式训练4.设集合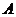 为函数
为函数 的定义域,集合
的定义域,集合 为函数
为函数 的值域,集合
的值域,集合 为不等式
为不等式 的解集.(1)求
的解集.(1)求 ;(2)若
;(2)若 ,求
,求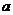 的取值范围.
的取值范围.
解:(1)解得A=(-4,2), B= 。 所以
。 所以
|
 <0
<0
3. ,
,
 ,
,
2. =
,
=
, =
,
=
, .
.
1.A∩A=
,A∩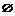 =
,A∩B=
,B∩A,A∪A=
,
=
,A∩B=
,B∩A,A∪A=
,
A∪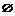 = ,A∪B=B∪A
= ,A∪B=B∪A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com