
2、已知 是虚数单位,若
是虚数单位,若 ,则
,则 的值等于
的值等于
A.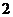 B.
B. C.
C.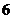 D.
D.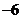
1、若集合 ,
, ,则
,则
A. B.
B. C.
C.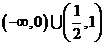 D.
D.
22、(本题满分14分)
已知数列 满足
满足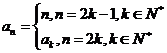 ,记
,记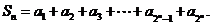
(1)求 ;
;
(2)证明 ;
;

 w_w w. k#s5_
w_w w. k#s5_
(3)求 ,并证明
,并证明 。
。




21、(本题满分12分)

 高☆考♂资♀源?网 ☆
高☆考♂资♀源?网 ☆
设 是函数
是函数 的两个极值点,且
的两个极值点,且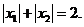
(1)求 与
与 的关系式;
的关系式;

 w_w w. k#s5_
w_w w. k#s5_
(2)令函数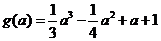 ,求函数
,求函数 的值域.
的值域.
20、(本题满分12分)
双曲线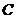 与椭圆
与椭圆 有相同的焦点,直线
有相同的焦点,直线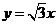 为双曲线
为双曲线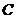 的一条渐近线
的一条渐近线
(1)求双曲线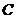 的方程;
的方程;
(2)过点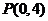 的直线
的直线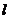 交双曲线
交双曲线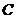 于
于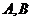 两点,交
两点,交 轴于
轴于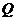 点(点
点(点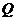 与
与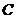 的顶点不重合)。当
的顶点不重合)。当 ,且
,且 时,求直线
时,求直线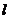 的方程。
的方程。
19、(本题满分12分)
 已知梯形
已知梯形 中,
中, 分别是
分别是 上的点,
上的点,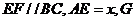 是
是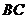 的中点。沿
的中点。沿 梯形
梯形 翻折,使平面
翻折,使平面 平面
平面 (如图)。
(如图)。
(1)当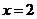 时,求证:
时,求证: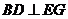 ;
;

 w_w w. k#s5_
w_w w. k#s5_
(2)若以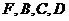 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为 ,求
,求 的最大值;
的最大值;
⑶当 取得最大值时,求二面角
取得最大值时,求二面角 的余弦值。
的余弦值。
18、(本题满分12分)
某社区举办2010年上海世博会知识宣传活动,进行现场抽奖,抽奖规则是:盒中装有10张大小相同的精美卡片,卡片上分别印有“世博会会徽”或“海宝”( 世博会吉祥物)图案,参加者每次从盒中抽取卡片两张,若抽到的两张都是“海宝” 卡即可获奖。
(1)
活动开始后,一位参加者问:“盒中有几张‘海宝’
卡?”,主持人笑说:“我只知道从盒中任抽两张都不是‘海宝’卡的概率是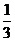 ”,求抽奖都获奖的概率;
”,求抽奖都获奖的概率;
(2) 在(1)的条件下,现在甲、乙、丙、丁四人依次抽奖,抽后放回,另一个人再抽,求至多有一人获奖的概率。
17、(本题满分12分)

 高☆考♂资♀源?网 ☆
高☆考♂资♀源?网 ☆
已知函数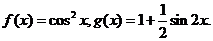
(1)设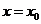 是函数
是函数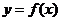 的图象的一条对称轴,求
的图象的一条对称轴,求 的值;
的值;
(2)求函数 的值域。
的值域。

 w_w w. k#s5_
w_w w. k#s5_
16、在 中,
中, 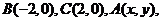 给出
给出 满足的条件,就能得到动点
满足的条件,就能得到动点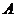 的轨迹方程,下表给出了一些条件和一些方程:
的轨迹方程,下表给出了一些条件和一些方程:

 w_w w. k#s5_
w_w w. k#s5_

则满足条件1、2、③的轨迹方程分别为______________(用代号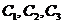 填入)。
填入)。
15、设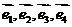 是平面内的四个单位向量,其中
是平面内的四个单位向量,其中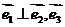 与
与 的夹角为
的夹角为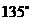 ,对这个平面内的任一个向量
,对这个平面内的任一个向量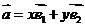 ,规定经过一次“斜二测变换”得到向量
,规定经过一次“斜二测变换”得到向量 ,设向量
,设向量 ,则经过一次“斜二测变换”得到向量
,则经过一次“斜二测变换”得到向量 的模
的模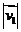 是_____________________.
是_____________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com