
4.a1,a2,…,a2n+1成等差数列,且下标为奇数的项的和为60,下标为偶数的项的和为45,则该数列的项数是
3.若数列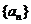 是等差数列,首项
是等差数列,首项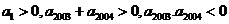 ,则使前n项和
,则使前n项和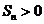 成立的最大自然数n是:
( )
成立的最大自然数n是:
( )
A .4005 , B 4006, C. 4007 , D .4008
[填空题]
2.设Sn是等差数列{an}的前n项和,若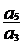 =
=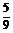 ,则
,则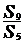 =
( )
=
( )
A 1 B -1 C 2 D 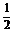
1.在等比数列{an}中,a5+a6=a(a≠0),a15+a16=b,则a25+a26的值是 ( )
A.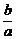 B.
B.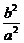 C.
C.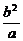 D.
D.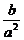
2.转化化归思想.函数方程思想;重点是运用所学知识综合解决问题的能力.
例题简答
同步练习 3.6等差等比数列综合
[选择题]
1.等差与等经数列的综合,数列与函数、不等式、方程、等内容的综合.
[例1](2005北京海淀模拟)在等比数列{an}(n∈N*)中,a1>1,公比q>0.设bn=log2an,且b1+b3+b5=6,b1b3b5=0.
(1)求证:数列{bn}是等差数列;
(2)求{bn}的前n项和Sn及{an}的通项an;
(3)试比较an与Sn的大小.
剖析:(1)定义法即可解决.(2)先求首项和公差及公比.(3)分情况讨论.
(1)证明:∵bn=log2an,∴bn+1-bn=log2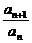 =log2q为常数.∴数列{bn}为等差数列且公差d=log2q.
=log2q为常数.∴数列{bn}为等差数列且公差d=log2q.
(2)解:∵b1+b3+b5=6,∴b3=2.
∵a1>1,∴b1=log2a1>0.
∵b1b3b5=0,∴b5=0.
∴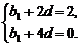 解得
解得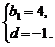
∴Sn=4n+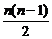 ×(-1)=
×(-1)=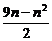 .
.
∵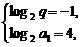 ∴
∴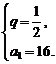
∴an=25-n(n∈N*).
(3)解:显然an=25-n>0,当n≥9时,Sn=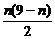 ≤0.
≤0.
∴n≥9时,an>Sn.
∵a1=16,a2=8,a3=4,a4=2,a5=1,a6=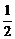 ,a7=
,a7=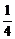 ,a8=
,a8=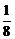 ,S1=4,S2=7,S3=9,S4=10,S5=10,S6=9,S7=7,S8=4,
,S1=4,S2=7,S3=9,S4=10,S5=10,S6=9,S7=7,S8=4,
∴当n=3,4,5,6,7,8时,an<Sn;
当n=1,2或n≥9时,an>Sn.
评述:本题主要考查了数列的基本知识和分类讨论的思想.
[例2](2002春北京)已知点的序列An(xn,0),n∈N*,其中xl=0,x2=a(a>0),A3是线段AlA2的中点,A4是线段A2A3的中点,…,An是线段An-2An-1的中点,….
(1)写出xn与xn-1、xn-2之间的关系式(n≥3);
(2)设an=xn+1-xn,计算al,a2,a3,由此推测数列{an}的通项公式,并加以证明.
解:(1)当n≥3时,xn=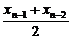 .
.
(2)a1=x2-x1=a,a2=x3-x2=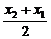 -x2=-
-x2=-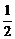 (x2-x1)=-
(x2-x1)=-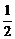 a,
a,
a3=x4-x3=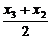 -x3=-
-x3=-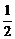 (x3-x2)=-
(x3-x2)=-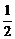 (-
(-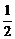 a)=
a)=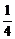 a,
a,
由此推测:an=(-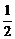 )n-1a(n∈N*).
)n-1a(n∈N*).
证明如下:因为a1=a>0,且an=xn+1-xn=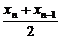 -xn=
-xn=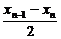 =-
=-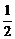 (xn-xn-1)=-
(xn-xn-1)=-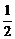 an-1(n≥2),所以an=(-
an-1(n≥2),所以an=(-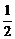 )n-1a.
)n-1a.
[例3] 已知f(x)=(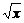 +
+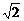 )2(x≥0),又数列{an}(an>0)中,a1=2,这个数列的前n项和的公式Sn(n∈N*)对所有大于1的自然数n都有Sn=f(Sn-1).
)2(x≥0),又数列{an}(an>0)中,a1=2,这个数列的前n项和的公式Sn(n∈N*)对所有大于1的自然数n都有Sn=f(Sn-1).
(1)求数列{an}的通项公式;
(2)若bn=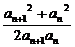 (n∈N*),求证
(n∈N*),求证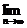 (b1+b2+…+bn-n)=1.
(b1+b2+…+bn-n)=1.
解:(1)∵f(x)=(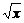 +
+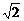 )2,
)2,
∴Sn=(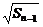 +
+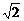 )2.
)2.
∴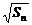 -
-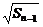 =
=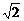 .又
.又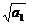 =
=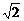 ,
,
故有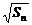 =
=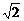 +(n-1)
+(n-1)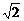 =n
=n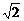 ,
,
即Sn=2n2(n∈N*).
当n≥2时,an=Sn-Sn-1=2n2-2(n-1)2=4n-2;
当n=1时,a1=2,适合an=4n-2.
因此,an=4n-2(n∈N*).
(2)∵bn=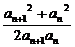 =1+
=1+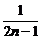 -
-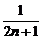 ,
,
∴b1+b2+b3+…+bn-n=1-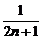 .
.
从而 (b1+b2+…+bn-n)=
(b1+b2+…+bn-n)= (1-
(1-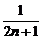 )=1.
)=1.
温馨提示:由于已知条件给出的是Sn与Sn-1的函数关系,求出Sn就可求出an.
[例4](2005北京东城模拟)已知等差数列{an}的首项a1=1,公差d>0,且第二项、第五项、第十四项分别是等比数列{bn}的第二项、第三项、第四项.
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}对任意正整数n均有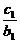 +
+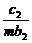 +
+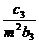 +…+
+…+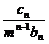 =(n+1)an+1成立,其中m为不等于零的常数,求数列{cn}的前n项和Sn.
=(n+1)an+1成立,其中m为不等于零的常数,求数列{cn}的前n项和Sn.
解:(1)由题意得(a1+d)(a1+13d)=(a1+4d)2,整理得2a1d=d2.
∵a1=1,解得d=2(d=0不合题意舍去),
∴an=2n-1(n=1,2,3,…).
由b2=a2=3,b3=a5=9,易求得bn=3n-1(n=1,2,3,…).
(2)当n=1时,c1=6;
当n≥2时,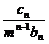 =(n+1)an+1-nan=4n+1,
=(n+1)an+1-nan=4n+1,
∴cn=(4n+1)mn-1bn=(4n+1)(3m)n-1.
∴cn=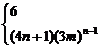
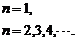
当3m=1,即m=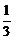 时,
时,
Sn=6+9+13+…+(4n+1)
=6+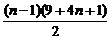
=6+(n-1)(2n+5)=2n2+3n+1.
当3m≠1,即m≠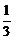 时,
时,
Sn=c1+c2+…+cn,即
Sn=6+9·(3m)+13·(3m)2+…+(4n-3)(3m)n-2+(4n+1)(3m)n-1. ①
3mSn=6·3m+9·(3m)2+13·(3m)3+…+(4n-3)(3m)n-1+(4n+1)(3m)n. ②
①-②得
(1-3m)Sn=6+3·3m+4·(3m)2+4·(3m)3+…+4·(3m)n-1-(4n+1)(3m)n
=6+9m+4[(3m)2+(3m)3+…+(3m)n-1]-(4n+1)(3m)n
=6+9m+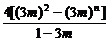 -(4n+1)(3m)n.
-(4n+1)(3m)n.
∴Sn=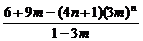 +
+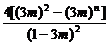 .
.
∴Sn=
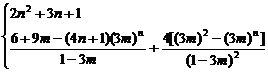

温馨提示(1)已知→公差→an和b,进而求出通项n;
(2)→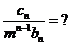 →Cn→Sn.
→Cn→Sn.
[研讨.欣赏]已知{an}是首项为2,公比为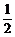 的等比数列,Sn为它的前n项和,
的等比数列,Sn为它的前n项和,
(1)用Sn表示Sn+1;
(2)是否存在自然数c和k,使得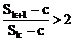 成立。
成立。
解:(1)∵ 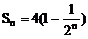
∴ 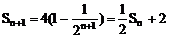
(2)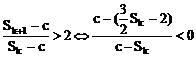 (*)
(*)
∵ 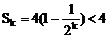
∴ 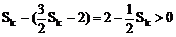
∴ 式(*)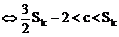 ①
①
∵ Sk+1>Sk
∴ 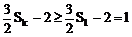
又Sk<4
∴ 由①得:c=2或c=3
当c=2时
∵ S1=2
∴ k=1时,c<Sk不成立,从而式①不成立
∵ 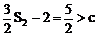
∴ 由Sk<Sk+1得:
∴ 当k≥2时,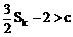 ,从而式①不成立
,从而式①不成立
当c=3时,S12,S2=3
∴ 当k=1,2时,C<Sk不成立
∴ 式①不成立
∵ 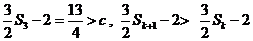
∴ 当k≥3时,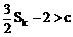 ,从而式①不成立
,从而式①不成立
综上所述,不存在自然数c,k,使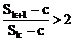 成立
成立
6. an=5-an-1, a18=3; 当n为偶数时,Sn=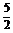 n;当n为奇数时,Sn=
n;当n为奇数时,Sn=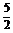 n-
n-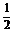 。
。
5.只需选取首项不为0,公比为-1的等比数列.答案:a,-a,a…(a≠0)
4.当k分别取1,2,3,4,5,6,7,8时,a3k+1分别与数列中的第4项,第7项,第2项,第5项,第8项,第3项,第6项,第1项相等,故{a3k+1}能取遍前8项.答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com