
8.已知函数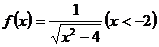 , (1)求
, (1)求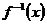
(2)
设 设
设 是否存在最小的正整数k,使对任意
是否存在最小的正整数k,使对任意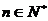 有
有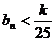 成立?若存在,求出k的值,若不存在,说明理由?
成立?若存在,求出k的值,若不存在,说明理由?
解:(1)由题
(2)由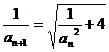 得
得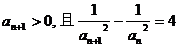
所以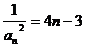 即
即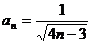
(3)先证明{bn}是单调递减数列,所以要对任意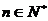 有
有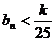 成立
成立
只须满足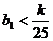 即可,解得存在最小的正整数k=8满足条件。
即可,解得存在最小的正整数k=8满足条件。
7.设f(k)是满足不等式log2x+log2(3·2k-1-x)≥2k-1(k∈N*)的自然数x的个数.
(1)求f(k)的表达式;
(2)记Sn=f(1)+f(2)+…+f(n),Pn=n2+n-1,当n≤5时试比较Sn与Pn的大小.
解:(1)由不等式log2x+log2(3·2k-1-x)≥2k-1,得x(3·2k-1-x)≥22k-1,解之得2k-1≤x≤2k,故f(k)=2k-2k-1+1=2k-1+1.
(2)∵Sn=f(1)+f(2)+…+f(n)=1+2+22+23+…+2n-1+n=2n+n-1,
∴Sn-Pn=2n+n-1-(n2+n-1)=2n-n2.
又n≤5,可计算得S1>P1,S2=P2,S3<P3,S4=P4,S5>P5.
6.由a32=a2·a6,得公差d=-2a1,故
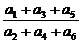 ==
==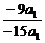 =
=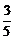 .答案:
.答案: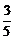
[解答题]
5.a1+a2=x+y;xy=b1·b2.
∴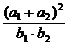 =
=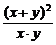 =
=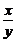 +
+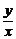 +2.
+2.
答案:[4,+∞)或(-∞,0]
4.7.(直接列方程)
3.a2003>0,a2004<0,a2003+a2004>0
则a1+a4006>0,故S4006>0.S4007<0.
法二:二次函数Sn的对称轴在2003和2004之间,靠近2003,故S4006>0,S2007<0.
2.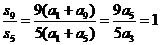 ;
;
1.由等比数列的性质得三个和成等比数列;
6.公差不为零的等差数列{an}的第二、三及第六项构成等比数列,则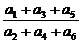 =_____.
=_____.
简答提示: 1-3.CAB;
5.若数列x,a1,a2,y成等差数列,x,b1,b2,y成等比数列,则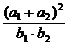 的取值范围是___________________.
的取值范围是___________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com