
2.(04年黄冈二轮)设x、y、z中有两条直线和一个平面,已知命题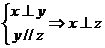 为真命题,则x、y、z中可能为平面的是
。
为真命题,则x、y、z中可能为平面的是
。
1.(04年广州综合测试)设命题p:∣4x-3∣≤1;命题q: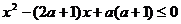 。若非p是非q的必要而不充分条件,则实数a的取值范围是
。
。若非p是非q的必要而不充分条件,则实数a的取值范围是
。
例1.下列说法:①2x+5>0;②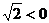 ;③如果x>2,那么
;③如果x>2,那么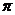 就是有理数;④如果x
就是有理数;④如果x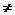 0,那么
0,那么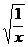 就有意义.一定是命题的说法是………………………………………………………………………( )
就有意义.一定是命题的说法是………………………………………………………………………( )
(A) ①② (B) ①③④ (C) ②③④ (D) ①②③.
例2.设有两个命题:
(1)关于x的不等式x2+(a-1)x+a2>0的解集是R;
(2)f(x)=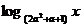 是减函数.且(1)和(2)至少有一个为真命题, 求实数a的取值范围.
是减函数.且(1)和(2)至少有一个为真命题, 求实数a的取值范围.
例3. 已知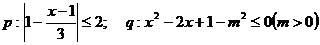 ,若﹁p 是﹁q的必要不充分条件,求实数m的取值范围.
,若﹁p 是﹁q的必要不充分条件,求实数m的取值范围.
3.命题甲:x+y≠3,命题乙:x≠1或y≠2.则甲是乙的 条件.
2.(05湖北卷)对任意实数a,b,c,给出下列命题:
①“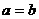 ”是“
”是“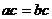 ”充要条件; ②“
”充要条件; ②“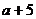 是无理数”是“a是无理数”的充要条件③“a>b”是“a2>b2”的充分条件;④“a<5”是“a<3”的必要条件.
是无理数”是“a是无理数”的充要条件③“a>b”是“a2>b2”的充分条件;④“a<5”是“a<3”的必要条件.
其中真命题的个数是 ( B )
A.1 B.2 C.3 D.4
1.(05天津卷)给出下列三个命题
①若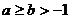 ,则
,则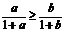
②若正整数m和n满足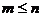 ,则
,则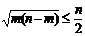
③设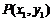 为圆
为圆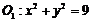 上任一点,圆O2以
上任一点,圆O2以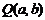 为圆心且半径为1.当
为圆心且半径为1.当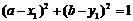 时,圆O1与圆O2相切
时,圆O1与圆O2相切
其中假命题的个数为 ( B )
A.0 B.1 C.2 D.3
8、反证法:从命题结论的反面出发(假设),引出(与已知、公理、定理…)矛盾,从而否定假设证明原命题成立,这样的证明方法叫做反证法。
7、如果已知p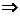 q那么我们说,p是q的充分条件,q是p的必要条件。
q那么我们说,p是q的充分条件,q是p的必要条件。
若p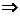 q且q
q且q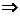 p,则称p是q的充要条件,记为p⇔q.
p,则称p是q的充要条件,记为p⇔q.
6、四种命题之间的相互关系:
一个命题的真假与其他三个命题的真假有如下三条关系:(原命题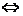 逆否命题)
逆否命题)
①、原命题为真,它的逆命题不一定为真。
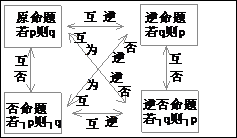 ②、原命题为真,它的否命题不一定为真。
②、原命题为真,它的否命题不一定为真。
③、原命题为真,它的逆否命题一定为真。
5、四种命题的形式:
原命题:若P则q; 逆命题:若q则p;
否命题:若┑P则┑q;逆否命题:若┑q则┑p。
(1)交换原命题的条件和结论,所得的命题是逆命题;
(2)同时否定原命题的条件和结论,所得的命题是否命题;
(3)交换原命题的条件和结论,并且同时否定,所得的命题是逆否命题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com