
3.碘酸钾是一种白色结晶粉末,无臭无味,酸性条件下碘酸钾是一种较强的氧化剂,与氢碘酸、二氧化硫等还原性物质作用,被还原为单质碘,在碱性介质中,碘酸钾能被氯气、次氯酸盐等氧化为高碘酸钾。碘酸钾在常温下稳定,加热至560℃开始分解。工业生产碘酸钾的流程如下,在反应器中发生反应的化学方程式为:6I2+11KClO3+3H2O=6KH(IO3)2+5KCl+3Cl2

(1)步骤①反应器发生的反应中,转移电子总数为 ;
(2)步骤②中,用硝酸而不用HI,其原因可能是
_______________________________________________;
(3)步骤③要保持溶液微沸1小时以完全排出氯气,排出氯气的原因为___________________________________;
(4)参照下表碘酸钾的溶解度,步骤11得到碘酸钾晶体,你建议的方法是_________________________________。
|
温度/℃ |
0 |
10 |
20 |
40 |
60 |
80 |
|
KIO3g/100g水 |
4.60 |
6.27 |
8.08 |
12.6 |
18.3 |
24.8 |
2.氯气是很重要的工业原料,很多化学物质成分中均含有氯,如饮用水消毒常用的消毒剂;三氯化磷是无色液体,是重要的化工原料,可用来制造许多磷的化合物,如敌百虫等多种农药。科学家舍勒在化学上的另一个重要的贡献是发现了氯气。一般情况下,在实验室中常用较强的氧化剂[如MnO2、PbO2、KMnO4、KClO3、Ca(ClO)2等]氧化盐酸制氯气。
(1)写出用PbO2和浓盐酸反应制备氯气时的化学方程式_________________________。铅元素在元素周期表中位置是__________________;已知PbO2是一种两性氧化物,试写出PbO2和NaOH浓溶液反应时的离子方程式 。
(2)现用漂粉精和浓盐酸反应制备氯气。将足量漂粉精投入浓盐酸中。反应中涉及到的化学方程式可能有 、 。
(3)磷在氯气中燃烧可生成无色液体PCl3和淡黄色晶体PCl5,PCl3还可继续与Cl2作用生成PCl5,PCl3和PCl5均可与水反应:PCl3+3H2O=H3PO3+3HCl,PCl5+H2O=POCl3+2HCl, PCl5+4H2O=H3PO4+5HCl。PCl5受热可分解:PCl5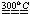 PCl3+Cl2。
PCl3+Cl2。
①将红磷(P)与Cl2按规定2:5物质的量之比放在密闭容器中,加热至5000C发生反应,所得产物主要是_______________;
②已知PCl3分子为三角锥形结构,键角为1000,H3PO3与足量NaOH溶液作用的产物是Na2HPO3,则在下列物质的分子中各原子的最外层均达到了八个电子结构的是___________。
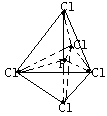 A.PCl3 B.PCl5 C.Na2HPO3 D.Na3PO4
A.PCl3 B.PCl5 C.Na2HPO3 D.Na3PO4
③已知PCl5分子为三角双锥结构的非极性分子,则PCl3F2有_____种同分异构体。
④水在液态时存在H3O+和OH-,液氨中存在少许NH4+和NH2-,PCl5在一定条件下也存在类似水和氨的解离方式,其中一种离子呈四面体结构。则两种离子分别是_______和________。
1.国家环保总局“2006年环境监测公报”指出,减少SO2的排放和生活废水的处理是我国“十一五”期间环境保护的主要任务。请回答下列问题:
(1)SO2的排放是造成酸雨的主要因素。某地区酸雨pH随时间的变化如下图所示。请用化学方程式表示该地区酸雨pH随时间增加而减小的原因 。
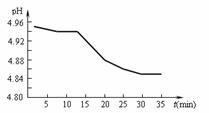
(2)新型氨法烟气脱硫技术采用氨吸收烟气中SO2生成亚硫酸铵和亚硫酸氢铵,再用一定量的磷酸进行反应,在反应回收SO2后的混合物中通入适量的氨气得到一种产品。该技术的优点是 。
(3)为进一步减少SO2的污染并变废为宝,人们正在探索用CO还原SO2得到单质硫的方法来除去SO2。该方法涉及到的化学反应为:SO2+2CO=2CO2+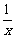 Sx 、CO+
Sx 、CO+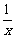 Sx=COS、2COS+SO2=2CO2+
Sx=COS、2COS+SO2=2CO2+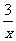 Sx 。其中COS分子的空间构型为 。
Sx 。其中COS分子的空间构型为 。
(4)生活污水中含大量细小的悬浮物,可加入某些物质使之聚集成较大的颗粒而沉淀。请你举一种常见的能使生活污水中悬浮物聚沉的物质,其化学式为 。若生活污水中含大量的氮化合物,通常用生物膜脱氮工艺进行处理:首先在消化细菌的作用下将NH4+氧化为NO3-:NH4++2O2=NO3-+2H++H2O,然后加入甲醇,NO3-和甲醇转化为两种无毒气体。请写出加入甲醇后反应的离子方程式 。
2.已知常温下,Mg(OH)2在其饱和溶液中的物质的量浓度为1.65×10-4 mol· L-1,Ag2O的溶解度是目1.6×10-3 g/100 g H2O,通过计算判断:
(1)将足量MgO和Ag2O分别放入水中,其水溶液能否使酚酞变红?(已知lg 3.3=0.5,l g 1.4=0.2)。
(2)取MgSO4稀溶液,加入适量NaHCO3稀溶液,并使NaHCO3与MgSO4的物质的量之比为2∶1,试回答:
①经检测,该溶液的pH=7.5,其原因是______________
_______________________________________________。
②在混合液中滴入酚酞,然后在水浴中加热至约60℃,其现象是___________,离子方程式是______________________________。待充分反应后,再升高温度在沸水浴中加热,其现象是___________,化学方程式是________________。
[课后巩固]
1.红矾(重铬酸钠Na2Cr2O7)是一种非常重要的工业产品;工业上生产红矾的工艺流程如下:①铬铁矿(可视为FeO·Cr2O3、还含有Al2O3、SiO2)与纯碱、石灰石混合后通过空气焙烧(使铬转化为+6价化合物)②焙烧产物加水后,并用硫酸调成中性溶液③过滤、滤液加硫酸酸化、浓缩、结晶成红矾。
(1)完成下列化学方程式:
SiO2+CaCO3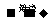 ;
;
Al2O3+Na2CO3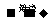 _____________________。
_____________________。
(2)配平下列反应方程式,填上系数:
FeO·Cr2O3+ Na2CO3+ O2 ¾
Na2CrO4+ Fe2O3+ CO2
(3)用水浸取焙烧产物,并用硫酸调成中性的目的是
,并写出有关的离子方程式 。
5.设平面α的一个法向量为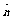 ,点P是平面α外一点,且Po∈α,则点P到平面α的距离是d=
,点P是平面α外一点,且Po∈α,则点P到平面α的距离是d=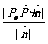 .
.
第2课时 空间向量的坐标运算
|
设a=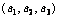 ,b=
,b=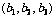
(1) a±b=
(2) 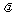 a= .
a= .
(3) a·b= .
(4) a∥b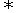 ;a
;a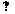 b
b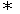 .
.
(5) 设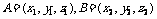
则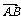 =
,
=
,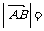 .
.
AB的中点M的坐标为 .
|
例1. 若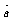 =(1,5,-1),
=(1,5,-1),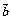 =(-2,3,5)
=(-2,3,5)
(1)若(k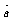 +
+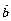 )∥(
)∥(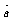 -3
-3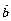 ),求实数k的值;
),求实数k的值;
(2)若(k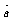 +
+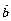 )⊥(
)⊥(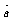 -3
-3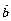 ),求实数k的值;
),求实数k的值;
(3)若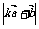 取得最小值,求实数k的值.
取得最小值,求实数k的值.
解:(1)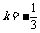 ;
;
(2)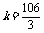 ; (3)
; (3)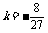
变式训练1. 已知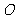 为原点,向量
为原点,向量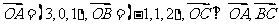 ∥
∥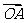 ,求
,求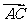 .
.
解:设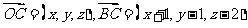 ,
,
∵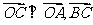 ∥
∥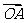 ,∴
,∴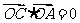 ,
,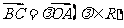 ,
,
∴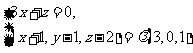 ,即
,即
解此方程组,得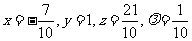 。
。
∴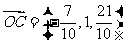 ,
,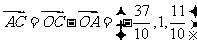 。
。
例2. 如图,直三棱柱 ,底面
,底面 中,CA=CB=1,
中,CA=CB=1,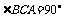 ,棱
,棱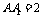 ,M、N分别A1B1、A1A是的中点.
,M、N分别A1B1、A1A是的中点.
(1) 求BM的长;
(2) 求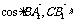 的值;
的值;
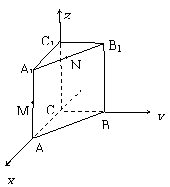 (3) 求证:
(3) 求证: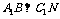 .
.
解:以C为原点建立空间直角坐标系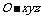 .
.
(1) 依题意得B(0,1,0),M(1,0,1).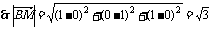 .
.
(2) 依题意得A1(1,0,2),B(0,1,0),C(0,0,0),B1(0,1,2).
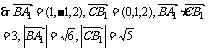
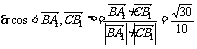 .
.
(3) 证明:依题意得C1(0,0,2),N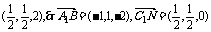 .
.
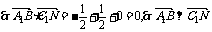
变式训练2. 在四棱锥P-ABCD中, 底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=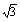 ,BC=1,PA=2,E为PD的中点.
,BC=1,PA=2,E为PD的中点.
(1) 在侧面PAB内找一点N,使NE⊥面PAC,并求出N点到AB和AP的距离;
(2) 求(1) 中的点N到平面PAC的距离.
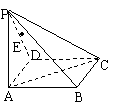
解:(1) 建立空间直角坐标系A-BDP,则A、B、C、D、P、E的坐标分别是A(0, 0, 0)、B(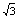 , 0, 0)、C(
, 0, 0)、C(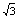 , 1, 0)、D(0, 1, 0)、P(0, 0, 2)、E(0,
, 1, 0)、D(0, 1, 0)、P(0, 0, 2)、E(0, 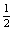 , 1),依题设N(x, 0, z),则
, 1),依题设N(x, 0, z),则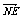 =(-x,
=(-x, 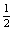 , 1-z),由于NE⊥平面PAC,
, 1-z),由于NE⊥平面PAC,
∴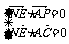
即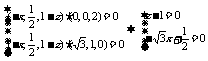
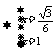 ,即点N的坐标为(
,即点N的坐标为(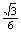 , 0, 1),
, 0, 1),
从而N到AB、AP的距离分别为1,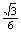 .
.
(2) 设N到平面PAC的距离为d,则d=
=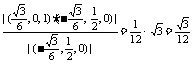 .
.
 例3. 如图,在底面是棱形的四棱锥
例3. 如图,在底面是棱形的四棱锥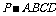 中,
中,
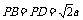 ,点E在
,点E在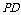 上,且
上,且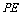 :
: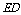 =2:1.
=2:1.
(1) 证明 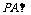 平面
平面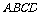 ;
;
(2) 求以AC为棱,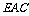 与
与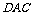 为面的二面角
为面的二面角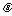 的大小;
的大小;
(3) 在棱PC上是否存在一点F,使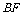 ∥平面
∥平面 ?证明你的结论.
?证明你的结论.
解:(1)证明略;
(2)易解得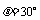 ;
;
(3)解 以A为坐标原点,直线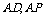 分别为y轴、z轴,过A点垂直于平面PAD的直线为x轴,建立空间直角坐标系(如图).由题设条件,相关各点的坐标为
分别为y轴、z轴,过A点垂直于平面PAD的直线为x轴,建立空间直角坐标系(如图).由题设条件,相关各点的坐标为
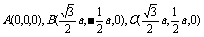
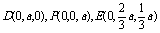
所以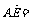
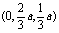 ,
,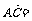
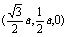 ,
,
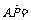
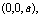
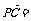
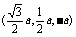
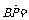
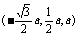 ,设点F是棱
,设点F是棱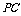 上的点,
上的点,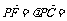
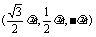 ,其中
,其中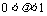 ,则
,则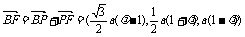 .令
.令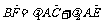 得
得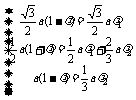
解得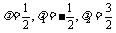 ,即
,即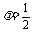 时,
时,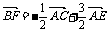 .亦即,F是PC的中点时,
.亦即,F是PC的中点时,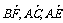 共面,又
共面,又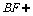 平面
平面 ,所以当F是PC的中点时,
,所以当F是PC的中点时,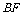 ∥平面
∥平面 .
.
例4. 如图,多面体是由底面为ABCD的长方体被截面AEFG所截而得,其中AB=4,BC=1,BE=3,CF=4.
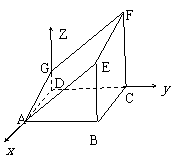 (1) 求
(1) 求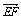 和点G的坐标;
和点G的坐标;
(2) 求GE与平面ABCD所成的角;
(3) 求点C到截面AEFG的距离.
解:(1) 由图可知:A(1,0,0),B(1,4,0),
E(1,4,3),F(0,4,4) ∴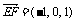
又∵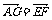 ,设G(0,0,z),则(-1,0,z)
,设G(0,0,z),则(-1,0,z)
=(-1,0,1) ∴z=1 ∴G(0,0,1)
(2)平面ABCD的法向量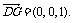
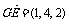 ,设GE与平面ABCD成角为
,设GE与平面ABCD成角为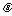 ,则
,则
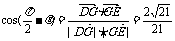
∴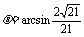
(3)设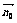 ⊥面AEFG,
⊥面AEFG,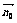 =(x0,y0,z0)
=(x0,y0,z0)
∵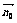 ⊥
⊥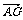 ,
,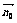 ⊥
⊥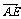 ,而
,而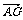 =(-1,0,1),
=(-1,0,1),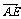 =(0,4,3)
=(0,4,3)
∴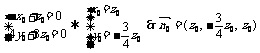
取z0=4,则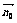 =(4,-3,4)
=(4,-3,4)
∵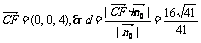
即点C到截面AEFG的距离为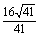 .
.
变式训练4. 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且PG=4,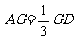 ,BG⊥GC,GB=GC=2,E是BC的中点.
,BG⊥GC,GB=GC=2,E是BC的中点.
(1)求异面直线GE与PC所成的角的余弦值;
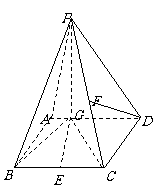 (2)求点D到平面PBG的距离;
(2)求点D到平面PBG的距离;
(3)若F点是棱PC上一点,且DF⊥GC,求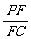 的值.
的值.
解:(1)以G点为原点,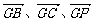 为x轴、y轴、
为x轴、y轴、
z轴建立空间直角坐标系,则B(2,0,0),C(0,2,0),
P(0,0,4),故E(1,1,0),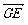 =(1,1,0),
=(1,1,0), 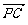 =(0,2,4)。
=(0,2,4)。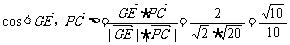 ,
,
∴GE与PC所成的余弦值为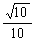 .
.
(2)平面PBG的单位法向量n=(0,±1,0) .
∵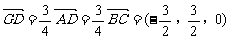 ,
,
∴点D到平面PBG的距离为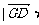 n |=
n |=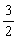 .
.
(3)设F(0,y,z),则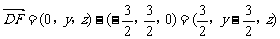 。
。
∵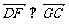 ,∴
,∴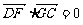 ,
,
即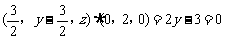 ,
,
∴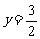 , 又
, 又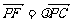 ,即(0,
,即(0,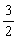 ,z-4)=λ(0,2,-4), ∴z=1,
,z-4)=λ(0,2,-4), ∴z=1,
|
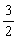 ,1) ,
,1) ,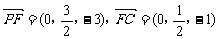 ,∴
,∴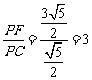 。
。
对于以下几类立体几何问题:(1) 共线与共面问题;(2) 平行与垂直问题;(3) 夹角问题;(4) 距离问题;(5) 探索性问题.
运用向量来解决它们有时会体现出一定的优势.用空间向量解题的关键步骤是把所求向量用某个合适的基底表示,本节主要是用单位正交基底表示,就是适当地建立起空间直角坐标系,把向量用坐标表示,然后进行向量与向量的坐标运算,最后通过向量在数量上的关系反映出向量的空间位置关系,从而使问题得到解决.在寻求向量间的数量关系时,一个基本的思路是列方程,解方程.
4.异面直线间的距离的向量求法:已知异面直线l1、l2,AB为其公垂线段,C、D分别为l1、l2上的任意一点,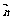 为与
为与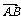 共线的向量,则|
共线的向量,则|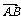 |=
|=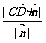 .
.
3.利用向量求夹角(线线夹角、线面夹角、面面夹角)有时也很方便.其一般方法是将所求的角转化为求两个向量的夹角,而求两个向量的夹角则可以利用公式cosθ=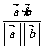 .
.
2.运用向量求解距离问题,其一般方法是找出代表相应距离的线段所对向量,然后计算这个向量对应的模.而计算过程中只要运用好加法法则,就总能利用一个一个的向量三角形,将所求向量用有模和夹角的已知向量表示出来,从而求得结果.
1.立体几何中有关垂直和平行的一些命题,可通过向量运算来证明.对于垂直,一般是利用a⊥b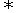 a·b=0进行证明.对于平行,一般是利用共线向量和共面向量定理进行证明.
a·b=0进行证明.对于平行,一般是利用共线向量和共面向量定理进行证明.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com