
2.下列变量之间的关系是函数关系的是 ( )
A.已知二次函数y=ax2+bx+c,其中,a,c是已知常数,取b为自变量,因变量是这个函数的判别式Δ=b2-4ac
B.光照时间和果树亩产量
C.降雪量和交通事故发生率
D.每亩施用肥料量和粮食亩产量
解析:由函数关系和相关关系的定义可知,①中Δ=b2-4ac,因为a、c是已知常数,b为自变量,所以给定一个b的值,就有唯一确定的Δ与之对应,所以Δ与b之间是一种确定的关系,是函数关系.②③④中两个变量之间的关系都是随机的、不确定的,所以不是函数关系.
答案:A
1.观察下列各图形:
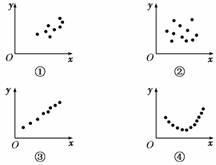
其中两个变量x、y具有相关关系的图是 ( )
A.①② B.①④ C.③④ D.②③
解析:相关关系有两种情况:所有点看上去都在一条直线附近波动,是线性相关;若所有点看上去都在某条曲线(不是一条直线)附近波动,是非线性相关.①②是不相关的.而③④是相关的.
答案:C
12.某单位有工程师6人,技术员12人,技工18人,要从这些人中抽取一个容量为n的样本.如果采用系统抽样法和分层抽样法抽取,不用剔除个体;如果样本容量增加一个,则在采用系统抽样时,需要在总体中先剔除1个个体.求样本容量n.
解:总体容量为6+12+18=36(人).当样本容量是n时,由题意知,系统抽样的间隔为,分层抽样的比例是,抽取工程师×6=(人),抽取技术员×12=(人),抽取技工×18=(人).所以n应是6的倍数,36的约数,即n=6,12,18,36.
当样本容量为(n+1)时,总体容量是35人,系统抽样的间隔为,因为必须是整数,所以n只能取6,即样本容量n=6.
11.(2010·福州模拟)下图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图,已知图中第一组的频数为4 000,请根据该图提供的信息解答下列问题:图中每组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500)

(1)求样本中月收入在[2 500,3 500)的人数.
(2)为了分析干部的收入与年龄、职业等方面的关系,必须从样本的各组中按月收入再用分层抽样方法抽出100人作进一步分析,则月收入在[1 500,2 000)的这段应抽多少人?
(3)试估计样本数据的中位数.
解:(1)∵月收入在[1 000,1 500)的概率为0.000 8×500=0.4,且有4 000人,
∴样本的容量n==10 000;月收入在[1 500,2 000)的频率0.000 4×500=0.2;
月收入在[2 000,2 500)的频率为0.000 3×500=0.15;
月收入在[3 500,4 000)的频率为0.000 1×500=0.05.
∴月收入在[2 500,3 500)的频率为1-(0.4+0.2+0.15+0.05)=0.15.
∴样本中月收入在[2 500,3 500)的人数为0.15×10 000=1 500.
(2)∵月收入在[1 500,2 000)的人数为0.2×10 000=2 000,
∴再从10 000人中用分层抽样方法抽出100人,则月收入在[1 500,2 000)的这段应抽取100×=20(人).
(3)由(1)知月收入在[1 000,2 000)的频率为0.4+0.2=0.6>0.5,
∴样本数据的中位数为1 500+=1 500+250=1 750(元).
10.某机构调查了当地1 000名居民的月收入,并根据所得数据画了样本的频率分布直方图,为了分析居民的收入与学历等方面的关系,要从这1 000人中再用分层抽样方法抽出100人做进一步调查,则在[2 500,3 000)(元)月收入段应抽样的人数是 ( )
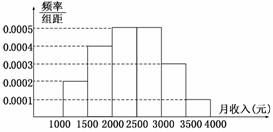
A.50 B.5 C.10 D.25
解析:本题为分层抽样与频率分布直方图的应用.由图知收入在[2 500,3 000)上的居民人数的频率为0.0005×500=0.25,故落在该区间的人数为1 000×0.25=250,若按分层抽样,由题知抽样比例为,故在[2 500,3 000)上抽取的居民人数为25.
答案:D
9.某企业三月中旬生产A、B、C三种产品共3 000件,根据分层抽样的结果,该企业统计员制作了如下的统计表格:
|
产品类别 |
A |
B |
C |
|
产品数量(件) |
|
1 300 |
|
|
样本容量(件) |
|
130 |
|
由于不小心,表格中A、C产品的有关数据已被污染看不清楚,统计员记得A产品的样本容量比C产品的样本容量多10,根据以上信息,可得C产品的数量是________件.
解析:设C产品的数量为x,则A产品的数量为1 700-x,C产品的样本容量为a,则A产品的样本容量为10+a,由分层抽样的定义可知:==,∴x=800.
答案:800
|
题组四 |
抽样方法的综合应用 |
8.(2009·湖南高考)一个总体分为A,B两层,用分层抽样方法从总体中抽取一个容量为10的样本.已知B层中每个个体被抽到的概率都为,则总体中的个体数为________.
解析:由分层抽样是等概率抽样得总体中的个体数为
10÷=120.
答案:120
7.(2009·陕西高考)某单位共有老、中、青职工430人,其中有青年职工160人,中年职工人数是老年职工人数的2倍.为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为 ( )
A.9 B.18 C.27 D.36
解析:设老年职工人数为x人,中年职工人数为2x,所以160+x+2x=430,得x=90.由题意老年职工抽取人数为=⇒y=18.
答案:B
6.某班级共有52名学生,现将学生随机编号,用系统抽样方法,抽取一个容量为4的样本,已知6号,32号,45号学生在样本中,那么在样本中还有一个学生的编号是________号.
解析:用系统抽样抽出的四个学生的号码从小到大成等差数列,因此,另一学生编号为6+45-32=19.
答案:19
|
题组三 |
分 层
抽 样 |
5.为了调查某产品的销售情况,销售部门从下属的92家销售连锁店中抽取30家了解情况.若用系统抽样法,则抽样间隔和随机剔除的个体数分别为 ( )
A.3,2 B.2,3 C.2,30 D.30,2
解析:因为92÷30不是整数,因此必须先剔除部分个体数,因为92=30×3+2,故剔除2个即可,而间隔为3.
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com