
4.如图是根据《山东统计年鉴2007》中的资料作成的1997年
至2006年我省城镇居民百户家庭人口数的茎叶图.图中左
边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为 ( )
A.304.6 B.303.6 C.302.6 D.301.6
解析:由已知得平均数
=
=303.6.
答案:B
3.(2010·合肥模拟)某中学一个高三数学教师对其所教的两个文科班(每班各50名学生)的学生的一次数学成绩进行了统计,高三年级文科数学平均分是100分,两个班数学成绩的频率分布直方图如下(总分:150分):
(1)文科1班数学平均分是否超过校平均分?
(2)从文科1班中任取一人,其数学成绩达到或超过校平均分的概率是多少?
(3)文1班一个学生对文2班一个学生说:“我的数学成绩在我班是中位数,从你班任抽一人的数学成绩不低于我的成绩的概率是0.60”,则文2班数学成绩在[100,110)范围内的人数是多少?

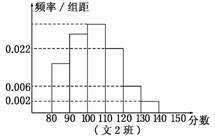
解:(1)文1班数学平均分至少是
=100.4,
文科1班数学平均分超过校平均分.
(2)文科1班在[100,110),[110,120),[120,130),[130,140),[140,150]分数段共有人数是33,从文科1班中任取一人,其数学成绩达到或超过校平均分的概率是P=0.66.
(3)设文1班这个学生的数学成绩是x,则x∈[100,110),
文2班数学成绩在[80,90)、[90,100)、[100,110)范围内的人数分别是b、c、y,
如果x=100,则=0.60,y=15,即文2班数学成绩在[100,110)范围内的人数至少是15人;
又∵,∴由②得:,
∴4+12+y≤35=b+c+y≤10+y-1+y⇒13≤y≤19,
则文2班数学成绩在[100,110)范围内的人数是15或16或17或18或19人.
|
题组二 |
茎叶图在估计总体中的应用 |

2.样本容量为200的频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在[6,10)内的频数为________,数据落在[2,10)内的概率约为________.
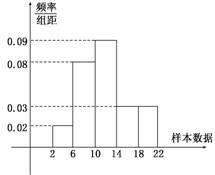
解析:由题易知样本数据落在[6,10)内的频数为200×0.08×4=64;数据落在[2,10)内的概率约为(0.02+0.08)×4=0.4.
答案:64 0.4
1.在样本的频率分布直方图中,一共有m(m≥3)个小矩形,第3个小矩形的面积等于其余m-1个小矩形面积之和的,且样本容量为100,则第3组的频数是 ( )
A.0.2 B.25 C.20 D.以上都不正确
解析:第3组的频率是,样本容量为100,
∴第3组的频数为100×=20.
答案:C
8.已知回归方程=4.4x+838.19,则可估计x与y的增长速度之比约为________.
解析:x与y的增长速度之比即为回归方程的斜率的倒数==.
7.对有线性相关关系的两个变量建立的回归直线方程=a+bx中,回归系数b ( )
A.可以小于0 B.大于0 C.能等于0 D.只能小于0
解析:因为b=0时,r=0,这时不具有线性相关关系,但b能大于0也能小于0.
答案:A
6.在一段时间内,某种商品价格x(万元)和需求量y(吨)之间的一组数据为:
|
价格x/万元 |
1.4 |
1.6 |
1.8 |
2 |
2.2 |
|
需求量y/吨 |
12 |
10 |
7 |
5 |
3 |
(1)画出散点图;
(2)求出y对x的回归直线方程,并在(1)的散点图中画出它的图象;
(3)如果价格定为1.9万元,预测需求量大约是多少(精确到0.01吨)?
解:(1)散点图,如图.

(2)采用列表的方法计算a与回归系数b.
|
序号 |
x |
y |
x2 |
Xy |
|
1 2 3 4 5 |
1.4 1.6 1.8 2 2.2 |
12 10 7 5 3 |
1.96 2.56 3.24 4 4.84 |
16.8 16 12.6 10 6.6 |
|
合计 |
9 |
37 |
16.6 |
62 |
=×9=1.8,=×37=7.4,
b==-11.5,
a=7.4+11.5×1.8=28.1,
y对x的回归直线方程为
=a+bx=28.1-11.5x.
(3)当x=1.9时,
y=28.1-11.5×1.9=6.25,
所以价格定为1.9万元时,需求量大约是6.25吨.
|
题组三 |
利用回归方程对总体进行估计 |
5.下表是某厂1-4月份用水量(单位:百吨)的一组数据,
|
月份x |
1 |
2 |
3 |
4 |
|
用水量y |
4.5 |
4 |
3 |
2.5 |
由其散点图知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程是=-0.7x+a,则a=________.
解析:=2.5,=3.5,
∴a=-b=3.5-(-0.7)×2.5=5.25.
答案:5.25
4.以下是两个变量x和y的一组数据:
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
y |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
则这两个变量间的线性回归方程为 ( )
A.=x2 B.= C.=9x-15 D.=15x-9
解析:根据数据可得=4.5,=25.5,
=204,iyi=1 296.
b=
 ==9,
==9,
a=-b=25.5-9×4.5=-15.
∴=9x-15.
答案:C
3.给出下列关系:
①正方形的边长与面积之间的关系;
②某化妆品的销售量与广告宣传费之间的关系;
③人的身高与视力之间的关系;
④雾天的能见度与交通事故的发生率之间的关系;
⑤学生与其学号之间的关系.
其中具有相关关系的是________.
解析:①正方形的边长与面积之间的关系是函数关系;
②化妆品的销售量与广告宣传费之间的关系不是严格的函数关系,但是具有相关性,因而是相关关系;
③人的身高与视力之间的关系既不是函数关系,也不是相关关系;
④能见度与交通事故的发生率之间具有相关关系;
⑤学生与其学号之间的关系是一种确定的对应关系.
综合以上可知,②④具有相关关系,而①⑤是确定性的函数关系.
答案:②④
|
题组二 |
求回归方程 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com