
6.在一项打鼾与患心脏病的调查中,共调查了1671人,经过计算K2=27.63,根据这一数据分析,我们有理由认为打鼾与患心脏病是________的(填“有关”或“无关”).
解析:K2>10.828,有99.9%的把握说打鼾与患心脏病有关.
答案:有关
5.冶炼某种金属可以用旧设备和改造后的新设备,为了检验用这两种设备生产的产品中所含杂质的关系,调查结果如下表所示:
|
|
杂质高 |
杂质低 |
|
旧设备 |
37 |
121 |
|
新设备 |
22 |
202 |
根据以上数据,则 ( )
A.含杂质的高低与设备改造有关
B.含杂质的高低与设备改造无关
C.设备是否改造决定含杂质的高低
D.以上答案都不对
解析:由已知数据得到如下2×2列联表
|
|
杂质高 |
杂质低 |
合计 |
|
旧设备 |
37 |
121 |
158 |
|
新设备 |
22 |
202 |
224 |
|
合计 |
59 |
323 |
382 |
由公式K2=≈13.11,
由于13.11>10.828,故有99.9%的把握认为含杂质的高低与设备是否改造是有关的.
答案:A
4.一般来说,一个人脚越长,他的身高就越高.现对10名成年人的脚长x与身高y进行测量,得如下数据(单位:cm):
|
x |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
y |
141 |
146 |
154 |
160 |
169 |
176 |
181 |
188 |
197 |
203 |
作出散点图后,发现散点在一条直线附近.经计算得到一些数据:
=24.5,=171.5,(xi-)(yi-)=577.5,
(xi-)2=82.5.
某刑侦人员在某案发现场发现一对裸脚印,量得每个脚印长26.5 cm,请你估计案发嫌疑人的身高为________ cm.
解析:由已知得===7,
=-=0,故=7x.当x=26.5时,y=185.5.
答案:185.5
|
题组二 |
独立性检验问题 |
3.关于线性回归,以下说法错误的是 ( )
A.自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系
B.在平面直角坐标系中用描点的方法得到的表示具有相关关系的两个变量的一组数据的图形叫做散点图
C.线性回归直线方程最能代表观测值x,y之间的关系
D.任何一组观测值都能得到具有代表意义的回归直线方程
解析:依据两个变量具有相关关系的意义可知,A正确;根据散点图的定义得B正确;根据最小二乘法的思想,所求得的回归直线,满足一组数据对应点到该直线的距离最小,即线性回归直线方程最能代表观测值x,y之间的关系,故C正确;D不正确.
答案:D
2.某人对一地区人均工资x(千元)与该地区人均消费y(千元)进行统计调查,y与x有相关关系,得到回归直线方程=0.66x+1.562.若该地区的人均消费额水平为7.675千元,估计该地区的人均消费额占人均工资收入的百分比约为 ( )
A.66% B.72% C.67% D.83%
解析:该题考查线性回归的实际应用.由条件知,消费水平为7.675千元时,人均工资为≈9.262(千元).故≈83%.
答案:D
1.由一组样本数据(x1,y1),(x2,y2),…,(xn,yn)得到回归直线方程=x+,那么下面说法错误的是 ( )
A.直线=x+必经过点(,)
B.直线=x+至少经过点(x1,y1),(x2,y2),…,(xn,yn)中的一个点
C.直线=x+的斜率=
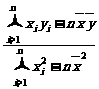
D.直线=x+和各点(x1,y1),(x2,y2),…,(xn,yn)的偏差yi-(xi+)]2是该坐标平面上所有直线与这些点的偏差中最小的
解析:回归直线方程=x+经过样本点的中心(,),可能不经过(x1,y1),(x2,y2),…,(xn,yn)中的任何一点,这些点分布在这条直线附近.
答案:B
8.(2009·江苏高考)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:
|
学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
|
甲班 |
6 |
7 |
7 |
8 |
7 |
|
乙班 |
6 |
7 |
6 |
7 |
9 |
则以上两组数据的方差中较小的一个为s2=________.
解析:由题中表格得,甲班:平均数甲=7,
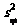 =(12+02+02+12+02)=;
=(12+02+02+12+02)=;
乙班:乙=7,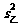 =(12+02+12+02+22)=.
=(12+02+12+02+22)=.
∵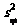 <
<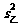 ,∴两组数据中方差较小的为s2=
,∴两组数据中方差较小的为s2=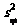 =.
=.
7.(2009·四川高考)设矩形的长为a,宽为b,其比满足b:a=≈0.618,这种矩形给
人以美感,称为黄金矩形.黄金矩形常应用于工艺品设计中.下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确结论是( )
A.甲批次的总体平均数与标准值更接近
B.乙批次的总体平均数与标准值更接近
C.两个批次总体平均数与标准值接近程度相同
D.两个批次总体平均数与标准值接近程度不能确定
解析:甲==0.617,
乙==0.613,
∴甲与0.618更接近.
答案:A
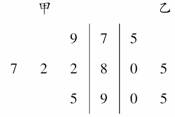
6.(2010·泉州模拟)甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5次预赛成绩记录如下:
甲 82 82 79 95 87
乙 95 75 80 90 85
(1)用茎叶图表示这两组数据;
(2)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(3)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.
解:(1)作出茎叶图如下:
(2)记甲被抽到的成绩为x,乙被抽到的成绩为y,用数对(x,y)表示基本事件:
(82,95),(82,75),(82,80),(82,90),(82,85),
(82,95),(82,75),(82,80),(82,90),(82,85),
(79,95),(79,75),(79,80),(79,90),(79,85),
(95,95),(95,75),(95,80),(95,90),(95,85),
(87,95),(87,75),(87,80),(87,90),(87,85).
基本事件总数n=25.
记“甲的成绩比乙高”为事件A,事件A包含的基本事件:
(82,75),(82,80),(82,75),(82,80),(79,75),(95,75),(95,80),(95,90),(95,85),(87,75),(87,80),(87,85).
事件A包含的基本事件数m=12.
所以P(A)==.
(3)派甲参赛比较合适.理由如下:
甲=(70×1+80×3+90×1+9+2+2+7+5)=85,
乙=(70×1+80×2+90×2+5+0+5+0+5)=85,
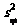 =[(79-85)2+(82-85)2+(82-85)2+(87-85)2+(95-85)2]=31.6,
=[(79-85)2+(82-85)2+(82-85)2+(87-85)2+(95-85)2]=31.6,
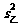 =[(75-85)2+(80-85)2+(85-85)2+(90-85)2+(95-85)2]=50.
=[(75-85)2+(80-85)2+(85-85)2+(90-85)2+(95-85)2]=50.
∵甲=乙,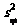 <
<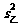 ,
,
∴甲的成绩较稳定,派甲参赛比较合适.
|
题组三 |
用样本的数字特征估计总体的数字特征 |
5.(2009·福建高考)某校开展“爱我海西、爱我家乡”摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是________.

解析:若茎叶图中的x对应的分数为最高分,
则有平均分=≈91.4≠91.故最高分应为94.
故去掉最高分94,去掉最低分88,其平均分为91,
∴=91,解得x=1.
答案:1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com