
8.甲、乙两名同学在五次考试中数学成绩统计用茎叶图表示如
右图所示,则下列说法正确的是 ( )
A.甲的平均成绩比乙的平均成绩高
B.甲的平均成绩比乙的平均成绩低
C.甲成绩的方差比乙成绩的方差大
D.甲成绩的方差比乙成绩的方差小
解析:由图可知甲的五次成绩分别为99,98,105,118,115,则可得甲成绩的平均数为107,方差为66.8;乙的五次成绩分别为95,106,108,112,114,则可得乙的平均成绩为107,方差为44.
答案:C
7.(2010·台州模拟)某工厂生产A、B、C三种不同型号的产品,产品的数量之比依次为3∶4∶7,现在用分层抽样的方法抽出容量为n的样本,样本中A型产品有15件,那么样本容量n为 ( )
A.50 B.60 C.70 D.80
解析:分层抽样要按比例抽取,A、B、C三种产品的数量之比为3∶4∶7,则抽取样本之比也应为3∶4∶7,所以A抽15件,B抽×4=20件,C抽×7=35件,故样本容量为15+20+35=70.
 答案:C
答案:C
6.某校对高三年级的学生进行体检,现将高三男生的体重(kg)数据进行整理后分成五组,并绘制频率分布直方图(如图所示).根据一般标准,高三男生的体重超过65 kg属于偏胖,低于55 kg属于偏瘦.已知图中从左到右第一、第三、第四、第五小组的频率分别为0.25,0.20,0.10,0.05,第二小组的频数为400,则该校高三年级的男生总数和体重正常的频率分别为 ( )
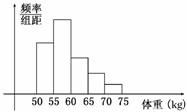
A.1000,0.50 B.800,0.50 C.800,0.60 D.1000,0.60
解析:据题意得第二小组的频率为1-(0.25+0.20+0.10+0.05)=0.4,且其频数为400,设高三年级男生总数为n,则有=0.4,∴n=1000,体重正常的学生所占的频率为第二和第三小组频率之和,即0.2+0.4=0.6.
答案:D
5.某篮球运动员在一个赛季的40场比赛中得分的茎叶图如图所示,则中位数与众数分别为 ( )

A.3与3 B.23与3 C.3与23 D.23与23
解析:众数是23,排列数据得中位数也是23.
答案:D
4.为了考察两个变量x、y之间的线性相关关系,甲、乙两同学各自独立地做10次和15次试验,并利用最小二乘法求得回归直线分别为l1和l2.已知在两人的试验中发现变量x的观测数据的平均值恰好相等,都为s,变量y的观测数据的平均值也恰好相等,都为t,那么下列说法中正确的是 ( )
A.直线l1,l2有交点(s,t)
B.直线l1,l2相交,但是交点未必是(s,t)
C.直线l1,l2由于斜率相等,所以必定平行
D.直线l1,l2必定重合
解析:由=x+,=-可知,当x=时,=,故回归方程过定点(,).所以回归直线l1过点(s,t),回归直线l2也过点(s,t),所以l1与l2有交点(s,t).
答案:A
3.一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是 ( )
A.57.2,3.6 B.57.2,56.4 C.62.8,63.6 D.62.8,3.6
解析:平均数增加60,即为62.8.
方差=(ai+60)-(+60)]2=(ai-)2=3.6.
答案:D
2.(2010·合肥模拟)现要完成下列3项抽样调查:
①从10盒酸奶中抽取3盒进行食品卫生检查.
②科技报告厅有32排,每排有40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请32名听众进行座谈.
③东方中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名.为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本.较为合理的抽样方法是 ( )
A.①简单随机抽样,②系统抽样,③分层抽样
B.①简单随机抽样,②分层抽样,③系统抽样
C.①系统抽样,②简单随机抽样,③分层抽样
D.①分层抽样,②系统抽样,③简单随机抽样
解析:①总体较少,宜用简单随机抽样;②已分段,宜用系统抽样;③各层间差距较大,宜用分层抽样.
答案:A
1.下列关系中,是相关关系的为 ( )
①学生的学习态度与学习成绩之间的关系;
②教师的执教水平与学生的学习成绩之间的关系;
③学生的身高与学生的学习成绩之间的关系;
④家庭的经济条件与学生的学习成绩之间的关系.
A.①② B.①③ C.②③ D.②④
解析:学生的学习成绩与学生的学习态度和教师的执教水平是相关的,与学生的身高和家庭经济条件不相关.
答案:A
8.某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
|
|
积极参加班级工作 |
不太主动参加班级工作 |
合计 |
|
学习积极性高 |
18 |
7 |
25 |
|
学习积极性一般 |
6 |
19 |
25 |
|
合计 |
24 |
26 |
50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关?并说明理由.
解:(1)积极参加班级工作的学生有24名,总人数为50名,概率为=.
不太主动参加班级工作且学习积极性一般的学生有19名,概率为.
(2)K2==≈11.5,
∵K2>10.828,
∴有99.9%的把握认为学习积极性与对待班级工作的态度有关系.
7.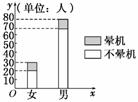 在一次飞机航程中调查男女乘客的晕机情况,男女乘客晕机
在一次飞机航程中调查男女乘客的晕机情况,男女乘客晕机
与不晕机的人数如右图所示.
(1)写出2×2列联表;
(2)判断晕机与性别是否有关?
解:(1)2×2列联表:
|
|
晕机 |
不晕机 |
合计 |
|
男 |
10 |
70 |
80 |
|
女 |
10 |
20 |
30 |
|
合计 |
20 |
90 |
110 |
(2)K2=≈6.37>5.024,
故有97.5%的把握认为“晕机与性别有关”.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com