
1.等差数列的概念和性质,证明数列{an}是等差数列的方法:
[例1](1)若一个等差数列前3项和为34,后3项和为146,且所有项的和为390,
求这个数列项数.
(2)等差数列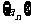 的前10项的和
的前10项的和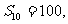 前100项的和
前100项的和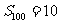 ,求前110项的和
,求前110项的和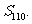
解(1)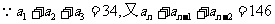
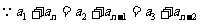
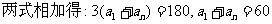 ,
,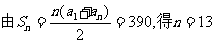
(2)分析一:方程的思想,将题目条件应用公式表示成关于首项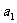 与公差
与公差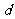 的两个方程.
的两个方程.
解法一:设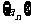 的首项为
的首项为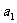 ,公差
,公差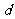 ,则
,则
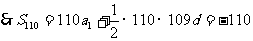
分析二:运用前n项和变式:
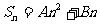
解法二:
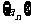 为等差数列,故可设
为等差数列,故可设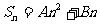 ,
,
则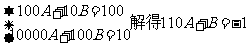
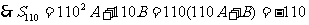
解法三: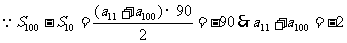
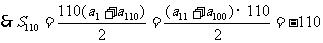
方法提炼:本题是等差数列的基本计算,要求熟练准确.
题(1)利用了等差数列的性质和前Sn公式的特点;
题(2)法一:转化为两个基本量,是重要的方法;法二利用了前n项和公式的函数式特征.
[例2]数列{an}的前n项和为Sn=npan(n∈N*)且a1≠a2,
(1)求常数p的值;
(2)证明:数列{an}是等差数列.
分析:(1)注意讨论p的所有可能值.
(2)运用公式an=
 求an.
求an.
解:(1)当n=1时,a1=pa1,若p=1时,a1+a2=2pa2=2a2,
∴a1=a2,与已知矛盾,故p≠1.则a1=0.
当n=2时,a1+a2=2pa2,∴(2p-1)a2=0.
∵a1≠a2,故p=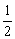 .
.
(2)由已知Sn=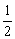 nan,a1=0.
nan,a1=0.
n≥2时,an=Sn-Sn-1=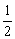 nan-
nan-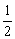 (n-1)an-1.
(n-1)an-1.
∴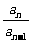 =
=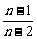 .则
.则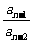 =
=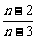 ,…,
,…,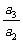 =
=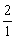 .(n≥3)
.(n≥3)
∴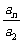 =n-1.∴an=(n-1)a2,
an-an-1=a2. (n≥3)
=n-1.∴an=(n-1)a2,
an-an-1=a2. (n≥3)
又a2-a1=a2,所以从第二项起每项减去前项的差是同一常数.
故{an}是以a2为公差,以a1为首项的等差数列.
提炼拓展: 证明等差数列的方法:1.由定义an-an-1=d, 2.等差中项,3.通项公式an=pn+q,4.Sn=Pn2=qn
例3.已知两个等差数列5,8,11,…和3,7,11…都有100项,问它们有多少相同的项?并求出所相同项的和。
分析一:两个等差数列的相同的项按原来的先后次序组成一个等差数列,且公差为原来两个公差的最小公倍数。
解:设两个数列相同项按原来的前后次序组成的新数列为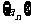 ,则
,则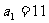
∵数列5,8,11,…和3,7,11…的公差分别为3与4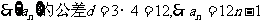
又因为数列5,8,11,…和3,7,11…的第100项分别是302和399,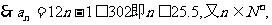 所以两个数列有25个相同的项。
所以两个数列有25个相同的项。
其和
分析二:由条件可知两个等差数列的通项公式,可用不定方程的求解法来求解。
解:设数列5,8,11,…和3,7,11…分别为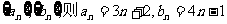
设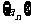 中的第n项与
中的第n项与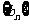 中的第m项相同,即
中的第m项相同,即
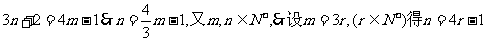
根据题意得:
从而有25个相同的项,且公差为12,其和
(另法:由m=3r知第r个相同的项为b3r=12r-1…)
方法提炼:法1:设两数列中an=bm,求出n(或m)应满足的关系,再代回an(或bm)
法2:两等差数列中相同的项成等差数列,且公差是两等差数列公差的最小公倍数.
例4、等差数列{an}中,前m项的和为77(m为奇数),其中偶数项的和为33,且a1-am=18,求这个数列的通项公式。
|
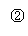 解法1:由已知
解法1:由已知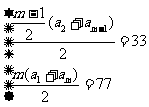
又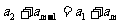 ,两式相除得
,两式相除得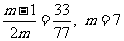 ,
,
从而由②得:a1+a7=22, 又已知 a1-a7=18,可解得 a1=20,a7=2.
公差d=-3, an=-3n+23.
解法2:利用前奇数项和与中项的关系
令m=2n-1,n∈N+
则 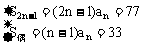
∴ 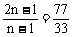 , n=4, m=7, an=11
, n=4, m=7, an=11
∴ a1+am=2an=22, 又a1-am=18
∴ a1=20,am=2
∴ d=-3
∴ an=-3n+23
提炼拓展;利用求和公式和性质;转化为两个基本量行吗?行.
[研讨.欣赏] 已知数列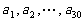 ,其中
,其中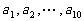 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;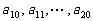 是公差为
是公差为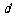 的等差数列;
的等差数列;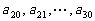 是公差为
是公差为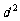 的等差数列(
的等差数列(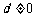 ). (1)若
). (1)若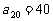 ,求
,求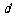 ;
;
(2)试写出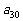 关于
关于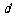 的关系式,并求
的关系式,并求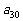 的取值范围;
的取值范围;
(3)续写已知数列,使得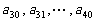 是公差为
是公差为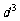 的等差数列,……,依次类推,把已知数列推广为无穷数列.
的等差数列,……,依次类推,把已知数列推广为无穷数列.
[解](1)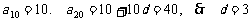 .
.
(2)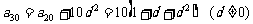 ,
,
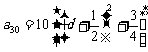 ,
,
当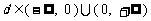 时,
时,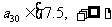 .
.
(3)所给数列可推广为无穷数列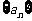 ,其中
,其中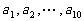 是首项为1,公差为1的等差数列,当
是首项为1,公差为1的等差数列,当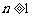 时,数列
时,数列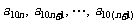 是公差为
是公差为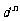 的等差数列.
的等差数列.
解题回顾:方法是基本的--转化为基本量,利用通项公式.题(3)考查类比的能力.
6.设首项为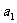 ,公差为
,公差为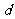 ,则
,则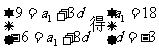
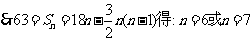
5.
a2+a4+a15=p(常数),∴3a1+18d=p,即a7=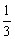 p.
p.
∴S13=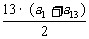 =13a7=
=13a7=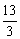 p.
p.
4.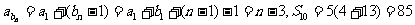
6.在等差数列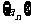 中,已知
中,已知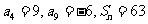 ,则n= .
,则n= .
简答:1-4.ACBC; 3. a11>|a10|=-a10,∴a10+a11=a1+a20>0.
∴S20=10(a1+a20)>0.选 B
5.等差数列{an}的前n项和记为Sn,若a2+a4+a15=p是一常数,则S13=
4.(2006天津)已知数列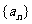 、
、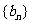 都是公差为1的等差数列,其首项分别为
都是公差为1的等差数列,其首项分别为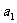 、
、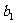 ,且
,且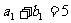 ,
,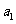 、
、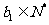 .设
.设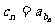 (
(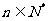 ),则数列
),则数列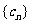 的前10项和等于
的前10项和等于
A.55 B.70 C.85 D.100 ( )
3.等差数列{an}中,a10<0,a11>0且a11>|a10|,Sn为其前n项和,则 ( )
A. S10小于0,S11大于0 B. S19小于0,S20大于0
C. S5小于0,S6大于0 D. S20小于0,S21大于0
2. (2006广东) 已知等差数列共有10项,其中奇数项之和15,偶数项之和为30,则其公差是 ( )
A 5 B 4 C 3 D 2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com